
(本题满分14分)在△ABC中,a、b、c分别是角A、B、C的对边,且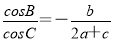 .
.
(1)求角B的大小;
(2)若b= ,a+c=4,求△ABC的面积.
,a+c=4,求△ABC的面积.
(1)B=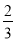 π;(2)
π;(2)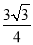 .
.
【解析】
试题分析:此题考查了正弦定理,余弦定理及三角函数的恒等变形.熟练掌握定理及公式是解本题的关键.利用正弦定理表示出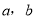 及
及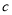 是第一问的突破点.
是第一问的突破点.
(1)根据正弦定理表示出a,b及c,代入已知的等式,利用两角和的正弦函数公式及诱导公式变形后,根据sinA不为0,得到cosB的值,由B的范围,利用特殊角的三角函数值即可求出角B的度数;(2)由(1)中得到角B的度数求出sinB和cosB的值,根据余弦定理表示出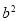 ,利用完全平方公式变形后,将b,a+c及cosB的值代入求出ac的值,然后利用三角形的面积公式表示出△ABC的面积,把ac与sinB的值代入即可求出值.
,利用完全平方公式变形后,将b,a+c及cosB的值代入求出ac的值,然后利用三角形的面积公式表示出△ABC的面积,把ac与sinB的值代入即可求出值.
试题解析:【解析】
(1)由正弦定理得: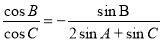 2分
2分
即 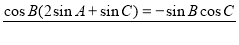
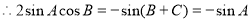
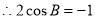
 B=
B=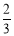 π, 7分
π, 7分
(2)由余弦定理得: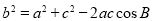
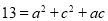 9分
9分
又a+c=4
解得: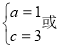
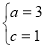 11分
11分
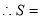
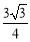 14分
14分
考点:1.正弦定理;2.余弦定理 .


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2014-2015学年湖南省醴陵市、四中高一上学期期中考试数学试卷(解析版) 题型:选择题
设偶函数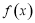 的定义域为
的定义域为 ,当
,当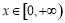 时
时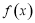 是增函数,则
是增函数,则 的大小关系是( )
的大小关系是( )
A.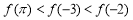
B.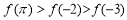
C.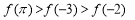
D.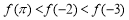
查看答案和解析>>
科目:高中数学 来源:2014-2015学年福建省高一上学期期中考试数学试卷(解析版) 题型:选择题
若偶函数 在区间
在区间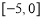 上是增函数且最小值为﹣4,则
上是增函数且最小值为﹣4,则 在区间
在区间 上是( )
上是( )
A.减函数且最小值为﹣4 B.增函数且最小值为﹣4
C.减函数且最大值为4 D.增函数且最大值为4
查看答案和解析>>
科目:高中数学 来源:2014-2015学年浙江省金华市高三上学期期中考试文科数学试卷(解析版) 题型:选择题
将函数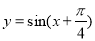 的图象上各点的横坐标伸长到原来2的倍,再向左平移
的图象上各点的横坐标伸长到原来2的倍,再向左平移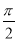 个单位,所得图象的函数解析式是( )
个单位,所得图象的函数解析式是( )
A.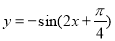
B.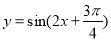
C.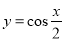
D.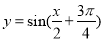
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com