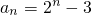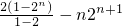Question

已知数列{a_n}中，a₁=-1，a_n+1=2a_n+3．
（1）若b_n=a_n+3，证明{b_n}是等比数列；
（2）求数列{a_n}的通项公式；
（3）若c_n=nb_n，求数列{c_n}的前n项和S_n．

Answer 1

（1）证明：∵a₁=-1，a_n+1=2a_n+3
∴a_n+1+3=2（a_n+3），a₁+3=2
∴b_n+1=2b_n
∴数列{b_n}是以2为首项，以2为公比的等比数列
（2）解：由（1）可得，b_n=
∴
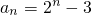
（3）解：∵c_n=nb_n=n•2ⁿ
∴s_n=1•2+2•2²+…+n•2ⁿ
2S_n=1•2²+2•2³+…+（n-1）•2ⁿ+n•2ⁿ⁺¹
两式相减可得，-s_n=2+2²+2³+…+2ⁿ-n•2ⁿ⁺¹
=
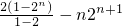
=（1-n）•2ⁿ⁺¹-2
∴s_n=（n-1）•2ⁿ⁺¹+2
分析：（1）由已知可得，a_n+1+3=2（a_n+3），即b_n+1=2b_n可证
（2）由（1）结合等比数列的通项公式可求
（3）由c_n=nb_n=n•2ⁿ，利用错位相减可求数列的和
点评：本题主要考查了利用数列的递推公式构造等比数列求解数列的通项公式，错位相减求数列的和的应用是求解的关键