
(本小题满分10分)
设数列 满足:
满足: .
.
(1)证明: 对
对 恒成立;
恒成立;
(2)令 ,判断
,判断 与
与 的大小,并说明理由.
的大小,并说明理由.
(1)证明略
(2)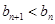
【解析】解:(1)证法一:当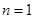 时,
时,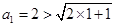 ,不等式成立,
,不等式成立,
假设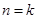 时,
时,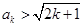 成立 (2分),
成立 (2分),
当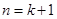 时,
时,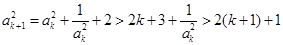 .(5分)
.(5分)
 时,
时,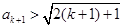 时成立
时成立
综上由数学归纳法可知, 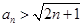 对一切正整数成立 (6分)
对一切正整数成立 (6分)
证法二:当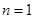 时,
时,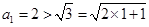 ,结论成立;
,结论成立;
假设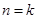 时结论成立,即
时结论成立,即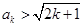 (2分) 当
(2分) 当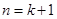 时,
时,
由函数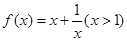 的单增性和归纳假设有
的单增性和归纳假设有
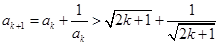 (4分),
(4分),
因此只需证: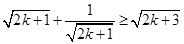 ,
,
而这等价于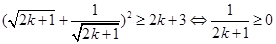 ,
,
显然成立,所以当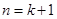 是,结论成立;
是,结论成立;
综上由数学归纳法可知, 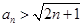 对一切正整数成立 (6分)
对一切正整数成立 (6分)
证法三:由递推公式得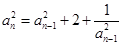 ,
,
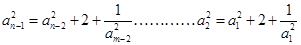 (2分)
(2分)
上述各式相加并化简得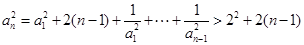
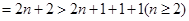 (4分)
(4分)
又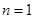 时,
时,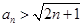 显然成立, 故
显然成立, 故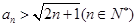 (6分)
(6分)
(2)解法一: (8分)
(8分)
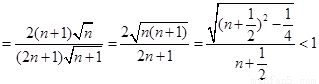 (10分)
(10分)
又显然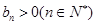 ,故
,故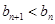 成立 (12分)
成立 (12分)
解法二: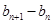
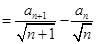
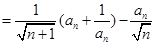
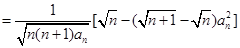
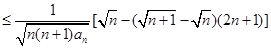 (由(1)的结论)(8分)
(由(1)的结论)(8分)
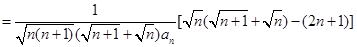 (10分)
(10分)
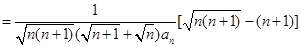
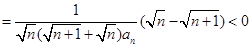
所以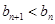 (12分)
(12分)
解法三: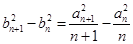
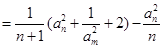 (8分)
(8分)
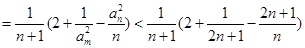 (10分)
(10分)
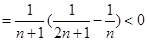
故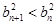 ,因此
,因此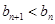 (12分)
(12分)


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
 (选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤.
(选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤.
|
|
| 1 |
| 2a |
| 1 |
| 2b |
| 1 |
| 2c |
| 1 |
| b+c |
| 1 |
| c+a |
| 1 |
| a+b |
查看答案和解析>>
科目:高中数学 来源: 题型:
 本题包括(1)、(2)、(3)、(4)四小题,请选定其中两题,并在答题卡指定区域内答,
本题包括(1)、(2)、(3)、(4)四小题,请选定其中两题,并在答题卡指定区域内答,
|
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com