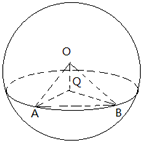
如图，点A、B都在半径为2的球上，圆Q是过A、B两点的截面，若A、B的球面距离为π，OQ=1，则三棱锥Q-ABO的体积等于

A.
$数学公式$
B.
$数学公式$
C.
$数学公式$
D.
3

C
分析：先根据A、B两点的球面距离为π，推出∠AOB= $\text{[math]}$ ，从而在直角三角形ABO中求出斜边AB的长，结合棱AQ，BQ的长，推出三棱锥的底面面积，然后求三棱锥Q-ABO的体积．
解答：由题意，A、B两点的球面距离为π．所以∠AOB= $\text{[math]}$ ，
在直角三角形ABO中，OA=OB=2，所以AB=2 $\text{[math]}$ ，
在直角三角形AQO和三角形BQO中，OA=OB=2，OQ=1，所以AQ=BQ= $\text{[math]}$ ，
在等腰三角形ABO中，底AB边长的高为1，
所以三棱锥Q-ABO的体积体积：V= $\text{[math]}$ × $\text{[math]}$ AB×1×OQ= $\text{[math]}$ ，
故选C
点评：本题考查球内接多面体、棱锥的体积，考查学生分析问题解决问题的能力，是基础题．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

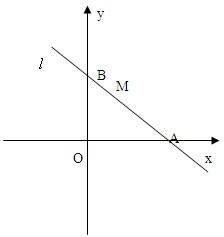已知直线l过点M（1，2），且直线l与x轴正半轴和y轴的正半轴交点分别是A、B，（如图，注意直线l与坐标轴的交点都在正半轴上）
（1）若三角形AOB的面积是4，求直线l的方程．
（2）求过点N（0，1）且与直线m垂直的直线方程．

查看答案和解析>>

科目：高中数学 来源： 题型：

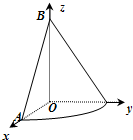如图，直角三角形OAB的直角顶点O是空间坐标系O-xyz的原点，点A在Ox轴正半轴上，|OA|=1；点B在Oz轴正半轴上，|OB|=2．我们称△OAB绕Oz轴逆时针旋转

后得到的旋转体为四分之一圆锥体．以下关于此四分之一圆锥体的三视图的表述错误的是（　　）

A、该四分之一圆锥体主视图和左视图的图形是全等的直角三角形

B、该四分之一圆锥体俯视图的图形是一个圆心角为

的扇形

C、该四分之一圆锥体主视图、左视图和俯视图的图形都是扇形

D、该四分之一圆锥体主视图的图形面积大于俯视图的图形面积

查看答案和解析>>

科目：高中数学 来源： 题型：

10、如图，一个“凸轮”放置于直角坐标系X轴上方，其“底端”落在远点O处，一顶点及中心M在Y轴的正半轴上，它的外围由以正三角形的顶点为圆心，以正三角形的边长为半径的三段等弧组成

今使“凸轮”沿X轴正向滚动过程中，“凸轮”每时每刻都有一个“最高点”，其中心也在不断移动位置，则在“凸轮”滚动一周的过程中，将其“最高点”和“中心点”所形成的图形按上、下放置，应大致为（　　）

A、

B、

C、

D、

查看答案和解析>>

科目：高中数学 来源： 题型：

[选做题]在A、B、C、D四小题中只能选做2题，每小题10分，计20分．请把答案写在答题纸的指定区域内．
A．（选修4-1：几何证明选讲）
如图，圆O的直径AB=8，C为圆周上一点，BC=4，过C作圆的切线l，过A作直线l的垂线AD，D为垂足，AD与圆O交于点E，求线段AE的长．
B．（选修4-2：矩阵与变换）
已知二阶矩阵A有特征值λ₁=3及其对应的一个特征向量α1=

，特征值λ₂=-1及其对应的一个特征向量α2=

-1

，求矩阵A的逆矩阵A^-1．
C．（选修4-4：坐标系与参数方程）
以平面直角坐标系的原点O为极点，x轴的正半轴为极轴，建立极坐标系（两种坐标系中取相同的单位长度），已知点A的直角坐标为（-2，6），点B的极坐标为(4，

)，直线l过点A且倾斜角为

，圆C以点B为圆心，4为半径，试求直线l的参数方程和圆C的极坐标方程．
D．（选修4-5：不等式选讲）
设a，b，c，d都是正数，且x=

a2+b2

，y=

c2+d2

．求证：xy≥

(ac+bd)(ad+bc)

．

查看答案和解析>>

科目：高中数学 来源： 题型：

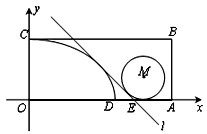在平面直角坐标系xOy中，矩形OABC的边OA、OC分别在x轴和y轴上（如图），且OC=1，OA=a+1（a＞1），点D在边OA上，满足OD=a．分别以OD、OC为长、短半轴的椭圆在矩形及其内部的部分为椭圆弧CD．直线l：y=-x+b与椭圆弧相切，与OA交于点E．
（1）求证：b²-a²=1；
（2）设直线l将矩形OABC分成面积相等的两部分，求直线l的方程；
（3）在（2）的条件下，设圆M在矩形及其内部，且与l和线段EA都相切，求面积最大的圆M的方程．

查看答案和解析>>

同步练习册答案