
(1)假设1992年底该城市堆积的垃圾为10万吨,从1993年到2002年这十年中,该城市每年产生的新垃圾以8%的年平均增长率增长,试求1993年该城市产生的新垃圾约有多少万吨?(精确到0.01,参考数据:1.0810≈2.159)
(2)如果从2003年起,该市每年处理上年堆积垃圾的20%,现有B1表示2003年底该市堆积的垃圾数量,B2表示2004年底该市堆积的垃圾数量,……,Bn表示2002+n年底该城市堆积的垃圾数量,①求B1;②试归纳出Bn的表达式(不用证明);③计算![]() ,并说明其实际意义.
,并说明其实际意义.
| (1)设1993年该城市产生的新垃圾为x万吨,依题意:
10+x+1.08x+1.082x+……+1.089x=50, ∴ ∴x= 所以,1993年该城市产生的新垃圾约为2.76万吨. (2)①B1=50×80%+3=43(万吨). ②∵B1=50×80%+3=50× B2= B3= ∴可归纳出Bn=50×( =50×( ③ 这说明,按题目设想的方法处理垃圾,该市垃圾总量将逐年减少,但不会少于15万吨. |


科目:高中数学 来源: 题型:
| lim | n→∞ |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| lim |
| n→∞ |
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)假设1992年底该城市堆积的垃圾为10万吨,从1993年到2002年这十年中,该城市每年产生的新垃圾以8%的年平均增长率增长,试求1993年该城市产生的新垃圾约有多少万吨?(精确到0.01,参考数据:1.0810≈2.159)
(2)如果从2003年起,该市每年处理上年堆积垃圾的20%,现有b1表示2003年底该市堆积的垃圾数量,b2表示2004年底该市堆积的垃圾数量,…,bn表示2002+n年底该城市堆积的垃圾数量,①求b1;②试归纳出bn的表达式(不用证明);③计算![]() bn,并说明其实际意义.
bn,并说明其实际意义.
查看答案和解析>>
科目:高中数学 来源:2006年高考第一轮复习数学:3.5 数列的应用(解析版) 题型:解答题
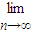 bn,并说明其实际意义.
bn,并说明其实际意义.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com