
| ||||
|
| ||||
|
| ||||
|
| 11 |
| 35 |
| ||||
|
| 3 |
| 35 |
| ||||
|
| ||||
|
| 8 |
| 35 |
| ||
|
| ||||||
|
| 13 |
| 35 |
| ||||
|
| ||||
|
| 8 |
| 35 |
| ||||
|
| 3 |
| 35 |
| X | 4 | 5 | 6 | 7 | 8 | ||||||||||
| P |
|
|
|
|
|
| 3 |
| 35 |
| 8 |
| 35 |
| 13 |
| 35 |
| 8 |
| 35 |
| 3 |
| 35 |


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| OP |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年山东省高三第六次(4月)周测理科数学试卷(解析版) 题型:解答题
在一个盒子中,放有大小相同的红、白、黄三个小球,现从中任意摸出一球,若是红球记1分,白球记2分,黄球记3分.现从这个盒子中有放回地先后摸出两球,所得分数分别记为 、
、 ,设
,设 为坐标原点,点
为坐标原点,点 的坐标为
的坐标为 ,记
,记 .
.
(1)求随机变量 =5的概率;
=5的概率;
(2)求随机变量 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源:2010年福建省八县(市高二下学期期末联考(理科)数学卷 题型:选择题
在一个盒子中有大小一样的 个球,其中
个球,其中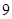 个红球,
个红球,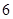 个白球,甲、乙两人各摸一球,不放回,则在甲摸出红球的条件下,乙摸出白球的概率为( )
个白球,甲、乙两人各摸一球,不放回,则在甲摸出红球的条件下,乙摸出白球的概率为( )
A.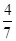 B.
B.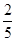 C.
C.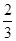 D.
D.
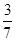
查看答案和解析>>
科目:高中数学 来源: 题型:
在一个盒子中,放有大小相同的红、白、黄三个小球,现从中任意摸出一球,若是红球记1分,白球记2分,黄球记3分.现从这个盒子中有放回地先后摸出两球,所得分数分别记为![]() 、
、![]() ,设
,设![]() 为坐标原点,点
为坐标原点,点![]() 的坐标为
的坐标为![]() ,记
,记![]() .
.
(1)求随机变量![]() =5的概率;
=5的概率;
(2)求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com