
【题目】已知椭圆![]() :
:![]() 的右焦点
的右焦点![]() ,且经过点
,且经过点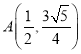 .
.
(1)求椭圆![]() 的方程;
的方程;
(2)点![]() 是坐标原点,若直线
是坐标原点,若直线![]() 与椭圆
与椭圆![]() 相切,过
相切,过![]() 作
作![]() ,垂足为
,垂足为![]() ,求证:
,求证:![]() 为定值.
为定值.
科目:高中数学 来源: 题型:
【题目】等比数列{an}的各项均为正数,且2a1+3a2=1, ![]() =9a2a6.
=9a2a6.
(1)求数列{an}的通项公式;
(2)设bn=log3a1+log3a2+…+log3an,求数列![]() 的前n项和.
的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】手机是人们必不可少的工具,极大地方便了人们的生活、工作、学习,现代社会的衣食住行都离不开它.某调查机构调查了某地区各品牌手机的线下销售情况,将数据整理得如下表格:
品牌 |
|
|
|
|
|
| 其他 |
销售比 |
|
|
|
|
|
|
|
每台利润(元) | 100 | 80 | 85 | 1000 | 70 | 200 |
该地区某商场岀售各种品牌手机,以各品牌手机的销售比作为各品牌手机的售出概率.
(1)此商场有一个优惠活动,每天抽取一个数字![]() (
(![]() ,且
,且![]() ),规定若当天卖出的第
),规定若当天卖出的第![]() 台手机恰好是当天卖出的第一台
台手机恰好是当天卖出的第一台![]() 手机时,则此
手机时,则此![]() 手机可以打5折.为保证每天该活动的中奖概率小于0.05,求
手机可以打5折.为保证每天该活动的中奖概率小于0.05,求![]() 的最小值;(
的最小值;(![]() ,
,![]() )
)
(2)此商场中一个手机专卖店只出售![]() 和
和![]() 两种品牌的手机,
两种品牌的手机,![]() ,
,![]() 品牌手机的售出概率之比为
品牌手机的售出概率之比为![]() ,若此专卖店一天中卖出3台手机,其中
,若此专卖店一天中卖出3台手机,其中![]() 手机
手机![]() 台,求
台,求![]() 的分布列及此专卖店当天所获利润的期望值.
的分布列及此专卖店当天所获利润的期望值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两名篮球队员轮流投篮直至某人投中为止,设甲每次投篮命中的概率为![]() ,乙每次投篮命中的概率为
,乙每次投篮命中的概率为![]() ,而且不受其他次投篮结果的影响.设投篮的轮数为
,而且不受其他次投篮结果的影响.设投篮的轮数为![]() ,若甲先投,则
,若甲先投,则![]() 等于( )
等于( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年4月26日,铁人中学举行了盛大的成人礼.仪式在《相信我们会创造奇迹》的歌声中拉开序幕,庄严而神圣的仪式感动了无数家长,4月27日,铁人中学官方微信发布了整个仪式精彩过程,几十年众志成城,数十载砥砺奋进,铁人中学正在创造着一个又一个奇迹.官方微信发布后,短短几个小时点击量就突破了万人,收到了非常多的精彩留言.学校从众多留言者中抽取了100人参加“学校满意度调查”,其留言者年龄集中在![]() 之间,根据统计结果,做出频率分布直方图如下:
之间,根据统计结果,做出频率分布直方图如下:

(Ⅰ)求这100位留言者年龄的样本平均数![]() 和样本方差
和样本方差![]() (同一组数据用该区间的中点值作代表);
(同一组数据用该区间的中点值作代表);
(Ⅱ)由频率分布直方图可以认为,留言者年龄![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 近似为样本均数
近似为样本均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() .
.
(ⅰ)利用该正态分布,求![]() ;
;
(ii)学校从年龄在![]() 和
和![]() 的留言者中,按照分层抽样的方法,抽出了7人参加“精彩留言”表彰大会,现要从中选出3人作为代表发言,设这3位发言者的年龄落在区间
的留言者中,按照分层抽样的方法,抽出了7人参加“精彩留言”表彰大会,现要从中选出3人作为代表发言,设这3位发言者的年龄落在区间![]() 的人数是
的人数是![]() ,求变量
,求变量![]() 的分布列和数学期望.附:
的分布列和数学期望.附:![]() ,若
,若![]() ,则
,则![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列4个结论:
①函数![]() 与函数
与函数![]() 的定义域相同,②函数
的定义域相同,②函数![]() (
(![]() 为常数)图像可由
为常数)图像可由![]() 的图像平移得到,③函数
的图像平移得到,③函数![]() 是奇函数且
是奇函数且![]() 是偶函数,④若幂函数
是偶函数,④若幂函数![]() 是奇函数,则
是奇函数,则![]() 是定义域上的增函数,其中正确的结论的序号是_________(将所有正确结论的序号都填上)
是定义域上的增函数,其中正确的结论的序号是_________(将所有正确结论的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况. 下列叙述中正确的是( )

A. 消耗1升汽油,乙车最多可行驶5千米
B. 以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多
C. 甲车以80千米/小时的速度行驶1小时,消耗10升汽油
D. 某城市机动车最高限速80千米/小时. 相同条件下,在该市用丙车比用乙车更省油
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 是
是![]() 的中点,
的中点, ![]() 在线段
在线段![]() 上,且满足
上,且满足![]() .
.

(1)求证: ![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 与平面
与平面![]() 所成角的余弦值是
所成角的余弦值是![]() ,若存在,求出
,若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com