
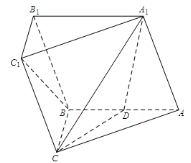
如图,在三棱柱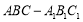 中,侧面
中,侧面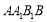 为菱形, 且
为菱形, 且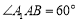 ,
,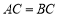 ,
,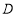 是
是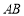 的中点.
的中点.
(1)求证:平面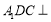 平面
平面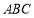 ;
;
(2)求证: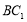 ∥平面
∥平面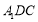 .
.
(1)详见解析,(2)详见解析.
【解析】
试题分析:(1)证明面面垂直,关键找出线面垂直.因为侧面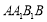 为菱形, 且
为菱形, 且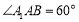 ,所以△
,所以△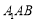 为正三角形,因而有
为正三角形,因而有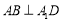 .又
.又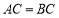 ,
,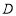 是
是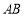 的中点,所以有
的中点,所以有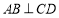 ,这样就可得到
,这样就可得到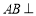 平面
平面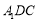 ,进而可证平面
,进而可证平面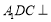 平面
平面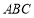 .(2)证明线面平行,关键找出线线平行. 条件“
.(2)证明线面平行,关键找出线线平行. 条件“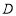 是
是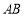 的中点”,提示找中位线.取
的中点”,提示找中位线.取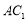 中点
中点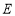 ,就可得
,就可得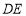 ∥
∥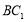 ,利用线面平行判断定理即可.解决此类问题,需注意写全定理成立的所有条件,不可省略.
,利用线面平行判断定理即可.解决此类问题,需注意写全定理成立的所有条件,不可省略.
试题解析:(1)证明:∵  为菱形,且
为菱形,且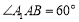 ,
,
∴△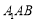 为正三角形. 2分
为正三角形. 2分

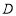 是
是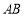 的中点,∴
的中点,∴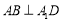 .
.
∵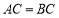 ,
,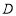 是
是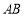 的中点,∴
的中点,∴ 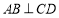 . 4分
. 4分

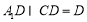 ,∴
,∴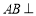 平面
平面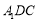 . 6分
. 6分
∵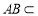 平面
平面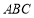 ,∴平面
,∴平面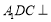 平面
平面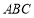 . 8分
. 8分
(2)证明:连结 ,设
,设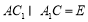 ,连结
,连结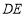 .
.
∵三棱柱的侧面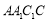 是平行四边形,∴
是平行四边形,∴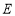 为
为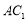 中点. 10分
中点. 10分
在△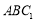 中,又∵
中,又∵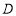 是
是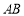 的中点,∴
的中点,∴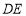 ∥
∥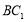 . 12分
. 12分
∵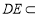 平面
平面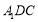 ,
,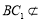 平面
平面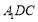 ,∴
,∴ 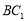 ∥平面
∥平面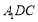 . 14分
. 14分
考点:面面垂直判定定理,线面平行判定定理


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2013-2014学年江苏省苏、锡、常、镇四市高三教学情况调查(一)理科数学试卷(解析版) 题型:解答题
甲乙两个同学进行定点投篮游戏,已知他们每一次投篮投中的概率均为 ,且各次投篮的结果互不影响.甲同学决定投5次,乙同学决定投中1次就停止,否则就继续投下去,但投篮次数不超过5次.
,且各次投篮的结果互不影响.甲同学决定投5次,乙同学决定投中1次就停止,否则就继续投下去,但投篮次数不超过5次.
(1)求甲同学至少有4次投中的概率;
(2)求乙同学投篮次数 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省苏、锡、常、镇四市高三教学情况调查(一)理科数学试卷(解析版) 题型:填空题
从甲,乙,丙,丁4个人中随机选取两人,则甲乙两人中有且只有一个被选取的概率为 .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省苏、锡、常、镇四市高三教学情况调查(一)文科数学试卷(解析版) 题型:填空题
一个容量为20的样本数据分组后,分组与频数分别如下: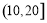 ,2;
,2;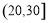 ,3;
,3;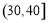 ,4;
,4;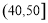 ,5;
,5; ,4;
,4;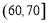 ,2.则样本在
,2.则样本在 上的频率是 .
上的频率是 .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省淮安市高三5月信息卷文科数学试卷(解析版) 题型:解答题
在平面直角坐标系 中,已知椭圆的焦点在
中,已知椭圆的焦点在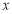 轴上,离心率为
轴上,离心率为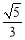 ,且经过点
,且经过点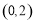 .
.
(1)求椭圆的标准方程;
(2) 以椭圆的长轴为直径作圆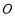 ,设
,设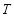 为圆
为圆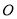 上不在坐标轴上的任意一点,
上不在坐标轴上的任意一点,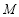 为
为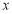 轴上一点,过圆心
轴上一点,过圆心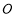 作直线
作直线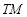 的垂线交椭圆右准线于点
的垂线交椭圆右准线于点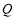 .问:直线
.问:直线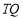 能否与圆
能否与圆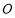 总相切,如果能,求出点
总相切,如果能,求出点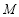 的坐标;如果不能,说明理由.
的坐标;如果不能,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com