
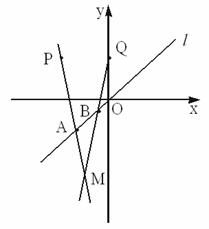
解:∵线段AB在直线l:y=x上,且线段AB的长为![]() ,
,
∴设M(x,y),A(t,t),B(t+1,t+1)(t为参数),则
直线PA的方程为y-2=![]() (x+2)(t≠-2), ①
(x+2)(t≠-2), ①
直线QB的方程为y-2=![]() x(t≠-1). ②
x(t≠-1). ②
∵M(x,y)是直线PA、QB的交点,
∴x、y是由①、②组成的方程组的解,由①、②消去参数t,得x2-y2+2x-2y+8=0. ③
当t=-2时,PA的方程为x=-2,QB的方程为3x-y+2=0,此时的交点为M(-2,-4).
当t=-1时,QB的方程为x=0,PA的方程为3x+y+4=0,
此时的交点为M(0,-4).
经验证,点(-2,-4)和(0,-4)均满足方程③.
故点M的轨迹方程为x2-y2+2x-2y+8=0.
点评:若不设参数,利用弦长公式来具体表示|AB|=![]() ,计算烦琐,不可取.应注意在变形过程中对参数的限制,做到过程中限之有理,答案准确无误.
,计算烦琐,不可取.应注意在变形过程中对参数的限制,做到过程中限之有理,答案准确无误.
弦长的巧妙转化、参数的设置与消去、特殊点的舍与补、交点的应用都体现了数形结合、等价转化等数学思想方法.


科目:高中数学 来源: 题型:
 已知两点P(-2,2),Q(0,2)以及一条直线:L:y=x,设长为
已知两点P(-2,2),Q(0,2)以及一条直线:L:y=x,设长为| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
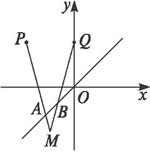
已知两点P(-2,2),Q(0,2)以及一条直线:L:y=x,设长为![]() 的线段AB在直线L上移动,如图。求直线PA和QB的交点M的轨迹方程。(要求把结果写成普通方程)
的线段AB在直线L上移动,如图。求直线PA和QB的交点M的轨迹方程。(要求把结果写成普通方程)

| |
| |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com