
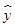 =
=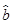 x+
x+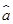 中的
中的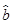 =2,则预测当气温为25 ℃时,冰糕销量为________箱.
=2,则预测当气温为25 ℃时,冰糕销量为________箱.| 气温/℃ | 18 | 13 | 10 | -1 |
| 冰糕/箱 | 64 | 38 | 34 | 24 |
科目:高中数学 来源:不详 题型:解答题
| PM2.5日均浓度 | 0~35 | 35~75 | 75~115 | 115~150 | 150~250 | >250 |
| 空气质量级别 | 一级 | 二级 | 三级 | 四级 | 五级 | 六级 |
| 空气质量类别 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 学历 | 35岁以下 | 35至50岁 | 50岁以上 |
| 本科 | 80 | 30 | 20 |
| 研究生 | x | 20 | y |
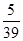 ,求x、y的值.
,求x、y的值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
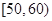 ,
,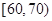 ,
,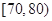 ,
,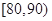 ,
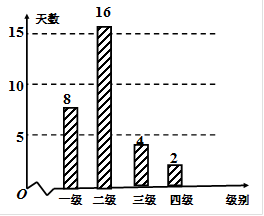
,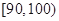 分别加以统计,得到如图所示的频率分布直方图.
分别加以统计,得到如图所示的频率分布直方图.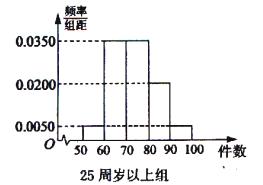
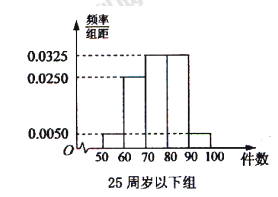

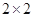 的列联表,并判断是否有
的列联表,并判断是否有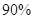 的把握认为“生产能手与工人所在的年龄组有关”?
的把握认为“生产能手与工人所在的年龄组有关”?
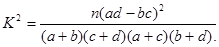
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 分组(体重) |  |  | 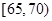 |  |
| 频数(人) |  |  |  |  |
 的频率;
的频率; 中共有几人?
中共有几人? 的人中,任取2人,求体重在
的人中,任取2人,求体重在 中各有1人的概率.
中各有1人的概率.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 分组 | 频数 | 频率 |
| [40,50) | 2 | 0.04 |
| [50,60) | 3 | 0.06 |
| [60,70) | 14 | 0.28 |
| [70,80) | 15[] | 0.30 |
| [80,90) | A | B |
| [90,100] | 4 | 0.08 |
| 合计 | C | D |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 年份 | 1985 | 1986 | 1987 | 1988 | 1989 | 1990 | 1991 | 1992 |
| x(kg) | 70 | 74 | 80 | 78 | 85 | 92 | 90 | 95 |
| y(t) | 5.1 | 6.0 | 6.8 | 7.8 | 9.0 | 10.2 | 10.0 | 12.0 |
| | ||||||||
| 年份 | 1993 | 1994 | 1995 | 1996 | 1997 | 1998 | 1999 | |
| x(kg) | 92 | 108 | 115 | 123 | 130 | 138 | 145 | |
| y(t) | 11.5 | 11.0 | 11.8 | 12.2 | 12.5 | 12.8 | 13.0 | |
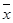 =101,
=101,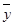 ≈10.113 3,
≈10.113 3,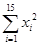 =161 125,
=161 125,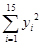 =1 628.55,
=1 628.55,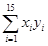 =16 076.8)
=16 076.8)查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
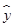 =0.66x+1.562(单位:千元),若某城市居民消费水平为7.675,估计该城市消费额占人均工资收入的百分比约为________.
=0.66x+1.562(单位:千元),若某城市居民消费水平为7.675,估计该城市消费额占人均工资收入的百分比约为________.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| | 又发作过心脏病 | 未发作过心脏病 | 合计 |
| 心脏搭桥手术 | 39 | 157 | 196 |
| 血管清障手术 | 29 | 167 | 196 |
| 合计 | 68 | 324 | 392 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com