
【题目】如图,四棱锥P﹣ABCD中,底面ABCD是直角梯形,∠DAB=90°AD∥BC,AD⊥侧面PAB,△PAB是等边三角形,DA=AB=2,BC![]() ,E是线段AB的中点.
,E是线段AB的中点.
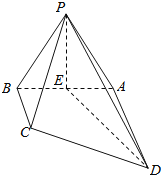
(1)求证:PE⊥CD;
(2)求PC与平面PDE所成角的正弦值.
【答案】(1)见解析;(2)![]()
【解析】
(1)先证明![]() ,再证明
,再证明![]() ,又
,又![]() ,推出PE⊥平面ABCD,然后证明PE⊥CD;
,推出PE⊥平面ABCD,然后证明PE⊥CD;
(2)以E为原点,建立如图所示的空间直角坐标系![]() ,推出
,推出![]() (2,1,0),
(2,1,0),![]() (0,0,
(0,0,![]() ),
),![]() (1,﹣1,
(1,﹣1,![]() ),设
),设![]() (x,y,z)为平面PDE的一个法向量,由
(x,y,z)为平面PDE的一个法向量,由 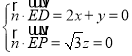 可以求得
可以求得![]() (1,﹣2,0),设PC与平面PDE所成的角为θ,利用
(1,﹣2,0),设PC与平面PDE所成的角为θ,利用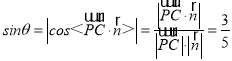 ,最后得出PC与平面PDE所成角的正弦值为
,最后得出PC与平面PDE所成角的正弦值为![]() .
.
(1)∵AD⊥侧面PAB,PE平面PAB,∴AD⊥EP.
又∵△PAB是等边三角形,E是线段AB的中点,∴AB⊥EP.
∵AD∩AB=A,∴PE⊥平面ABCD.
∵CD平面ABCD,∴PE⊥CD.
(2)以E为原点,EA、EP分别为y、z轴,建立如图所示的空间直角坐标系.
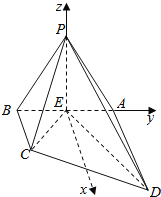
则E(0,0,0),C(1,﹣1,0),D(2,1,0),P(0,0,![]() ).
).
![]() (2,1,0),
(2,1,0),![]() (
(![]() ),
),![]() (1,﹣1,
(1,﹣1,![]() ).
).
设![]() (x,y,z)为平面PDE的一个法向量.
(x,y,z)为平面PDE的一个法向量.
由 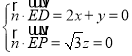 ,令x=1,可得
,令x=1,可得![]() (1,﹣2,0)
(1,﹣2,0)
设PC与平面PDE所成的角为θ,得
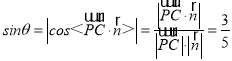
所以PC与平面PDE所成角的正弦值为![]() .
.


 高中必刷题系列答案
高中必刷题系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,有下列四个命题:
,有下列四个命题:
①函数![]() 是奇函数;
是奇函数;
②函数![]() 在
在![]() 是单调函数;
是单调函数;
③当![]() 时,函数
时,函数![]() 恒成立;
恒成立;
④当![]() 时,函数
时,函数![]() 有一个零点,
有一个零点,
其中正确的是____________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年最严环保使得各地空气质量指数(![]() )得到了很大的改善,2018年环保部将会更加突出大气、水、土壤三大领域污染治理,继续实施和深化环保领域改革,强化环境执法督察.某市设有12个空气监测站点,其中在轻度污染区、中度污染区、重度污染区分别设有3、6、3个监测点.以这12个站点测得的
)得到了很大的改善,2018年环保部将会更加突出大气、水、土壤三大领域污染治理,继续实施和深化环保领域改革,强化环境执法督察.某市设有12个空气监测站点,其中在轻度污染区、中度污染区、重度污染区分别设有3、6、3个监测点.以这12个站点测得的![]() 的平均值作为该市的空气质量指标.
的平均值作为该市的空气质量指标.
(Ⅰ)若某日的![]() 为120,已知测得轻度污染区的
为120,已知测得轻度污染区的![]() 的平均值为80,中度污染区
的平均值为80,中度污染区![]() 的平均值为116,求重度污染区
的平均值为116,求重度污染区![]() 的平均值;
的平均值;
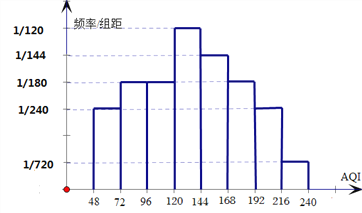
(Ⅱ)如图是2017年11月的30天的![]() 值的频率分布直方图,其中分段区间分别为
值的频率分布直方图,其中分段区间分别为![]() ,11月份仅有1天的
,11月份仅有1天的![]() 在
在![]() 之间.
之间.
①求11月的![]() 低于150的概率;
低于150的概率;
②双创活动中,验收小组要从中度污染区和重度污染区中按比例抽取六个监测点,然后从这六个监测点中随机抽取3个对监测数据进行核实,求至少抽到一个重度污染区的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十九世纪末:法国学者贝特朗在研究几何概型时提出了“贝特朗悖论”,即“在一个圆内任意选一条弦,这条弦的弦长长于这个圆的内接等边三角形边长的概率是多少?”贝特朗用“随机半径”“随机端点”“随机中点”三个合理的求解方法,但结果都不相同.该悖论的矛头直击概率概念本身,强烈地刺激了概率论基础的严格化.已知“随机端点”的方法如下:设![]() 为圆
为圆![]() 上一个定点,在圆周上随机取一点
上一个定点,在圆周上随机取一点![]() ,连接
,连接![]() ,所得弦长
,所得弦长![]() 大于圆
大于圆![]() 的内接等边三角形边长的概率.则由“随机端点”求法所求得的概率为( )
的内接等边三角形边长的概率.则由“随机端点”求法所求得的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列![]() 分别满足:
分别满足:![]() ,其中
,其中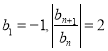 ,其中
,其中![]() ,设数列
,设数列![]() 前n项和分别为
前n项和分别为![]() .
.
(1)若数列![]() 为递增数列,求数列
为递增数列,求数列![]() 的通项公式;
的通项公式;
(2)若数列![]() 满足:存在唯一的正整数k(
满足:存在唯一的正整数k(![]() ),使得
),使得![]() ,则称
,则称![]() 为“k坠点数列”
为“k坠点数列”
(Ⅰ)若数列![]() 为“6坠点数列",求
为“6坠点数列",求![]() ;
;
(Ⅱ)若数列![]() 为“5坠点数列”,是否存在“p坠点数列”
为“5坠点数列”,是否存在“p坠点数列”![]() ,使得
,使得![]() ,若存在,求正整数m的最大值;若不存在,说明理由.
,若存在,求正整数m的最大值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 交于不同两点
交于不同两点![]() 、
、![]() ,直线
,直线![]() 、
、![]() 与抛物线的另一交点分别为两点
与抛物线的另一交点分别为两点![]() 、
、![]() ,连接
,连接![]() ,点
,点![]() 关于直线
关于直线![]() 的对称点为点
的对称点为点![]() ,连接
,连接![]() 、
、![]() .
.
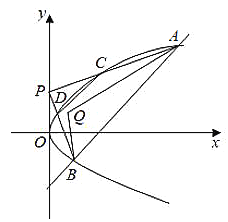
(1)证明:![]() ;
;
(2)若![]() 的面积
的面积![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com