已知数列{an}满足a1=7,an+1=3an+2n-1-8n.(n∈N*)
(Ⅰ)李四同学欲求{an}的通项公式,他想,如能找到一个函数f(n)=A•2n-1+B•n+C(A、B、C是常数),把递推关系变成an+1-f(n+1)=3[an-f(n)]后,就容易求出{an}的通项了.请问:他设想的f(n)存在吗?{an}的通项公式是什么?
(Ⅱ)记Sn=a1+a2+a3+…+an,若不等式Sn-2n2>p×3n对任意n∈N*都成立,求实数p的取值范围.
【答案】
分析:(Ⅰ)由题意a
n+1=3a
n+2
n-1-8n,要使函数f(n)=A•2
n-1+B•n+C(A、B、C是常数),把递推关系变成a
n+1-f(n+1)=3[a
n-f(n)],可得f(n+1)-3f(n)=2
n-1-8n,从而求出A,B;
(Ⅱ)记S
n=a
1+a
2+a
3+…+a
n,因为不等式S
n-2n
2>p×3
n对任意n∈N
*都成立,可得S
n-2n
2=3
n-2
n+4n,得出p与n的关系式,然后利用归纳法进行证明;
解答:解:(Ⅰ)∵a
n+1-f(n+1)=3[a
n-f(n)]
∴a
n+1=3a
n+f(n+1)-3f(n),
所以只需f(n+1)-3f(n)=2
n-1-8n,
∵f(n+1)-3f(n)=-A•2
n-1-2Bn+(B-2C),
∴-A=1,-2B=-8,B-2C=0,
∴A=-1,B=4,C=2.故李四设想的f(n)存在,f(n)=-2
n-1+4n+2.
∴a
n-f(n)=3
n-1[a
1-f(1)]=3
n-1(7-5)=2×3
n-1,
∴a
n=2×3
n-1+f(n)=2×3
n-1-2
n-1+2(2n+1).(5分)
(Ⅱ)S
n=2(1+3+3
2++3
n-1)-(1+2++2
n-1)+2[3+5++(2n+1)]=3
n-2
n+2n
2+4n.
∴S
n-2n
2=3
n-2
n+4n,(7分)
由S
n-2n
2>p×3
n,得
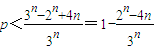
.
设
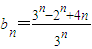
,则
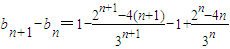
=
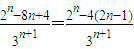
,
当n≥6时,2
n-2=(1+1)
n-2≥1+C
n-21+C
n-22++C
n-2n-3+C
n-2n-2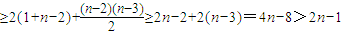
,
(用数学归纳法证也行)
∴n≥6时,b
n+1>b
n.容易验证,1≤n≤5时,b
n|+1<b
n,
∴p<(b
n)
min=
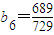
,
∴p的取值范围为
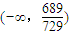
.(13分)
点评:此题是数学与不等式的综合,难度比较大,第一题根据(1)的思路进行求解,不是很难,第二问难度比较大,计算量也比较大,利用归纳法进行求解比较简单;

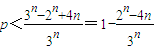 .
.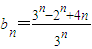 ,则
,则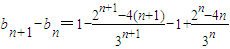 =
=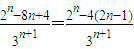 ,
,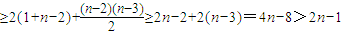 ,
,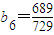 ,
,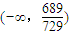 .(13分)
.(13分)

 轻松暑假总复习系列答案
轻松暑假总复习系列答案