
| A. | $y=x+\frac{1}{x}$,x≠0且x∈R | B. | $y=\frac{sinx}{2}+\frac{2}{sinx}$,x∈(0,π) | ||
| C. | $y=\frac{{{x^2}+3}}{{\sqrt{{x^2}+2}}}$,x∈R | D. | y=ex+e-x,x∈R |
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:高中数学 来源: 题型:解答题
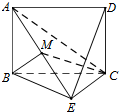 如图,已知矩形ABCD所在平面与等腰直角三角形BEC所在平面互相垂直,BE⊥EC,AB=BE,M为线段AE的中点.
如图,已知矩形ABCD所在平面与等腰直角三角形BEC所在平面互相垂直,BE⊥EC,AB=BE,M为线段AE的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,M,N分别是CC1,BC的中点,点p在直线A1B1上运动,且$\overrightarrow{{A}_{1}P}$=$λ\overrightarrow{{{A}_{1}B}_{1}}$(λ∈[0,1])
如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,M,N分别是CC1,BC的中点,点p在直线A1B1上运动,且$\overrightarrow{{A}_{1}P}$=$λ\overrightarrow{{{A}_{1}B}_{1}}$(λ∈[0,1])查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{4}$,1) | B. | (1,4) | C. | (1,8) | D. | (8,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com