
已知圆O的方程为 ,圆M的方程为
,圆M的方程为 ,过圆M上任意一点P作圆O的切线PA,若直线PA与圆M的另一个交点为Q,则当PQ的长度最大时,直线PA的斜率是___________.
,过圆M上任意一点P作圆O的切线PA,若直线PA与圆M的另一个交点为Q,则当PQ的长度最大时,直线PA的斜率是___________.
1或-7
解析试题分析:根据题意可以分析圆O的圆心到PA的距离为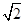 ,那么可知要使得在直角三角形QPA中,PQ最大,则只要OQ最大即可,那么即圆O的圆心到圆M上点的距离的最大值问题来处理,由于点|OM|为定值,且为
,那么可知要使得在直角三角形QPA中,PQ最大,则只要OQ最大即可,那么即圆O的圆心到圆M上点的距离的最大值问题来处理,由于点|OM|为定值,且为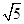 ,那么可知连接OM,则PA的长度结合勾股定理可知。那么设直线PA的斜率为k,那么PQ的中点与点M的连线的斜率为
,那么可知连接OM,则PA的长度结合勾股定理可知。那么设直线PA的斜率为k,那么PQ的中点与点M的连线的斜率为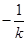 ,那么联立方程组可知其斜率为1或-7。
,那么联立方程组可知其斜率为1或-7。
考点:本试题考查了圆内弦的长度问题。
点评:要分析圆内弦的最值问题,可以结合圆的半径和弦心距,以及半弦长的关系来分析,这是解决该试题的关键,同时要利用两圆的位置关系,要使得PQ最大,只要点M到PA的距离最小即可。转化为点到直线的距离的最小值来进行,进而求得斜率值,属于中档题。


 备战中考寒假系列答案
备战中考寒假系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com