
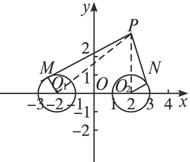
剖析:此题是以O1O2所在直线为x轴,线段O1O2的垂直平分线为y轴建立平面直角坐标系,把PM、PN的关系转化为PO1与PO2的关系,这样就把P、M、N三个动点问题转化为关于一个动点P的问题.
解:作直线O1O2,以直线O1O2为x轴,线段O1O2的垂直平分线为y轴,连结O1M、O2N,设P点坐标为(x,y).

∵PM、PN分别为⊙O1、⊙O2的切线,
∴O1M⊥PM,O2N⊥PN.
∴△PO1M,△PO2N为直角三角形.
∴PO12=PM2+O1M2=PM2+1,
PO22=PN2+O2N2=PN2+1.
∵PM=![]() PN,
PN,
∴PM2=2PN2.
∴PO12=2PN2+1, ①
2PO22=2(PN2+1)=2PN2+2. ②
由②-①得2PO22-PO12=1.
∵PO22=(x-2)2+y2,PO12=(x+2)2+y2,
∴2[(x-2)2+y2]-[(x+2)2+y2]=1.
∴2x2-8x+8+2y2-x2-4x-4-y2-1=0.
∴x2-12x+y2+3=0.
∴(x-6)2+y2=33.
讲评:正确建系是解好本题的首要任务,用PM、PN来表示PO1、PO2是本题的核心,这样就把三个动点问题转化为只关于一个动点P的问题.体现出转化思想的重要性,转化时用到了消去变量PM、PN的方法.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:
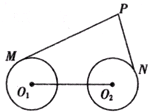 如图,圆O1与圆O2的半径都是1,O1O2=4,过动点P分别作圆O1.圆O2的切线PM、PN(M.N分别为切点),使得PM=
如图,圆O1与圆O2的半径都是1,O1O2=4,过动点P分别作圆O1.圆O2的切线PM、PN(M.N分别为切点),使得PM=| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 A.选修4-1:几何证明选讲
A.选修4-1:几何证明选讲
|
|
| α |
| α |
| β |
|
|
查看答案和解析>>
科目:高中数学 来源:2011-2012学年河北省高三第一次模拟考试理科数学试卷(解析版) 题型:解答题
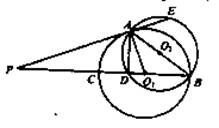
如图,圆O1与圆O2相交于A、B两点,AB是圆O2的直径,过A点作圆O1的切线交圆O2于点E,并与BO1的延长线交于点P,PB分别与圆O1、圆O2交于C,D两点.
求证:(Ⅰ)PA·PD=PE·PC;
(Ⅱ)AD=AE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com