
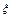 的概率分布如下:
的概率分布如下: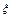 | 0 | 1 | 2 |
| P | 0.3 | 3k | 4k |
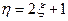 ,则
,则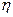 的数学期望为( )
的数学期望为( )| A.1.1 | B.3.2 | C.11k | D.22k+1 |
科目:高中数学 来源:不详 题型:解答题
 表示走出迷宫所需的时间.
表示走出迷宫所需的时间. 的分布列;
的分布列; 的数学期望.
的数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,若中奖,则家具城返还顾客现金1000元,某顾客购买一张价格为3400元的餐桌,
,若中奖,则家具城返还顾客现金1000元,某顾客购买一张价格为3400元的餐桌, 元;
元; 的所有可能取值;
的所有可能取值; 的分布列;
的分布列; 的期望E(
的期望E( );
);查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 。
。 ,求
,求 的分布列及期望。
的分布列及期望。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 元,若投保人在购买保险的一年度内出险,则可以获得10 000元的赔偿金.假定在一年度内有10 000人购买了这种保险,且各投保人是否出险相互独立.已知保险公司在一年度内至少支付赔偿金10 000元的概率为
元,若投保人在购买保险的一年度内出险,则可以获得10 000元的赔偿金.假定在一年度内有10 000人购买了这种保险,且各投保人是否出险相互独立.已知保险公司在一年度内至少支付赔偿金10 000元的概率为 。
。 ;
;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
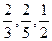 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
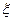 表示取出的3个小球上的最大数字,
表示取出的3个小球上的最大数字,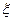 的概率分布和数学期望。
的概率分布和数学期望。查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ,且P(A)=m,设随机变量x=
,且P(A)=m,设随机变量x= 则x的方差D(x)是:( )
则x的方差D(x)是:( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com