
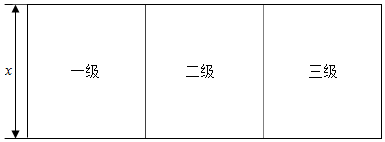
���� ������ˮ�����صĵ����һ�������Ϊx�ף��ɱ�ʾ�������Ӷ��ó���S����x�ĺ�������ʽ�������x��ȡֵ��Χ��
�������û�������ʽ�����Сֵ���ɣ�
��� �⣺����$S��x��=3x•2•138+200��3x•2+3•\frac{81}{x}•2��+70•81$=$12•��169x+\frac{8100}{x}��+5670$
=$2028x+\frac{97200}{x}+5670$������x��0����5�֣�
�����ɣ���
��x��0���ɻ�������ʽ��S��x��=$12•��169x+\frac{8100}{x}��+5670$$��12•2\sqrt{169x•\frac{8100}{x}}+5670$
=24•13•90+5670=28080+5670=33750����9�֣�
���ҽ���$169x=\frac{8100}{x}$����$x=\frac{90}{13}$ʱ��ȡ�Ⱥţ� ����10�֣�
��ʱ��Ϊ$\frac{81}{x}=11.7$����11�֣�
�൱��Ϊ11.7�ף���Ϊ$\frac{90}{13}$��ʱ��S��x����ͣ���������Ϊ33570Ԫ����12�֣�
���� ������Ҫ�����˽�����������ʽ�����û�������ʽ������ֵ��������ͬʱ������������������������е��⣮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | f��x��=x��g��x��=$\sqrt{{x}^{2}}$ | B�� | f��x��=x��g��x��=$\root{3}{{x}^{3}}$ | ||
| C�� | f��x��=cosx��g��x��=sin��$\frac{3��}{2}$+x�� | D�� | f��x��=lnx2��g��x��=2lnx |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 5 | B�� | 6 | C�� | 7 | D�� | 8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| x | 3 | 4 | 5 | 6 |
| y | 3 | 3.5 | 4.5 | 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 64 | B�� | 30 | C�� | 15 | D�� | 1 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com