
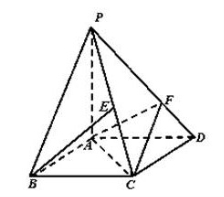
如图,四棱锥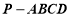 的底面
的底面 是平行四边形,
是平行四边形,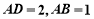 ,
,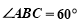 ,
,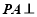 面
面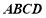 ,设
,设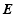 为
为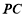 中点,点
中点,点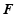 在线段
在线段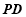 上且
上且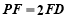 .
.
(1)求证: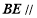 平面
平面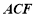 ;
;
(2)设二面角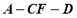 的大小为
的大小为 ,若
,若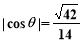 ,求
,求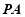 的长.
的长.
(1)证明详见解析;(2)2 .
【解析】
试题分析:(1)由已知条件用余弦定理和勾股定理推导出AB⊥AC.又PA⊥面ABCD,以AB,AC,AP分别为x,y,z轴建立坐标系.利用向量法能求出BE∥平面ACF.
(2)分别求出面PCD法向量和面ACF的法向量,由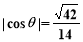 ,利用向量法能求出PA的长.
,利用向量法能求出PA的长.
(1)由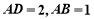 ,
,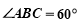 得
得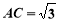 ,
,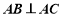 .
.
又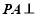 面
面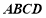 ,所以以
,所以以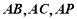 分别为
分别为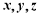 轴建立坐标系如图.
轴建立坐标系如图.
则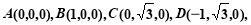 2分
2分
设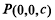 ,则
,则 .
.
设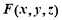 ,
,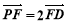 得:
得: 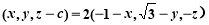 .
.
解得: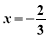 ,
,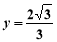 ,
,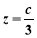 ,
,
所以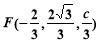 . 4分
. 4分
所以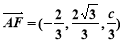 ,
,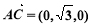 ,
,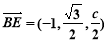 .
.
设面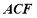 的法向量为
的法向量为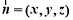 ,则
,则 ,取
,取 .
.
因为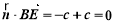 ,且
,且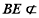 面
面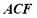 ,所以
,所以 平面
平面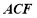 . 6分
. 6分
(2)设面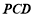 法向量为
法向量为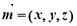 , 因为
, 因为 ,
,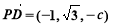 ,
,
所以 ,取
,取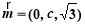 . 9分
. 9分
由 ,得
,得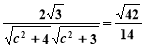 .
.
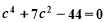 ,得
,得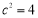 ,∴
,∴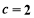 ,所以
,所以 . 12分
. 12分
考点:1.直线与平面平行的证明;2.线段长的求法.


科目:高中数学 来源:2013-2014学年江西省鹰潭市高三第二次模拟考试文科数学试卷(解析版) 题型:选择题
设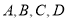 是平面直角坐标系中不同的四点,若
是平面直角坐标系中不同的四点,若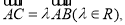
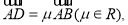 且
且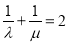 ,则称
,则称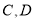 是关于
是关于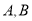 的“好点对”.已知
的“好点对”.已知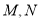 是关于
是关于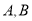 的“好点对”, 则下面说法正确的是( )
的“好点对”, 则下面说法正确的是( )
A.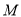 可能是线段
可能是线段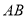 的中点
的中点
B.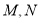 可能同时在线段
可能同时在线段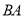 延长线上
延长线上
C.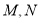 可能同时在线段
可能同时在线段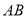 上
上
D.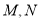 不可能同时在线段
不可能同时在线段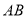 的延长线上
的延长线上
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西省鹰潭市高三第二次模拟考试文科数学试卷(解析版) 题型:选择题
已知条件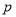 :
: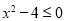 ,条件
,条件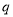 :
: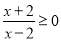 ,则
,则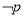 是
是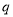 的( )
的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既非充分也非必要条件
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西省盟校高三第二次联考理科数学试卷(解析版) 题型:填空题
某大学的8名同学准备拼车去旅游,其中大一、大二、大三、大四每个年级各两名,分乘甲、乙两辆汽车。每车限坐4名同学(乘同一辆车的4名同学不考虑位置),其中大一的孪生姐妹需乘同一辆车,则乘坐甲车的4名同学中恰有2名同学是来自于同一年级的乘坐方式共有 种;
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西省盟校高三第二次联考理科数学试卷(解析版) 题型:选择题
以下四个命题中:
①从匀速传递的产品生产流水线上,质检员每10分钟从中抽取一件产品进行某项指标检测,这样的抽样是分层抽样;
②两个随机变量的线性相关性越强,相关系数的绝对值越接近于1;
③某项测量结果ξ服从正态分布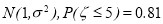 ,则
,则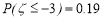 ;
;
④对于两个分类变量X与Y的随机变量k2的观测值k来说,k越小,判断“X与Y有关系”的把握程度越大.以上命题中其中真命题的个数为( )
A.4 B.3 C.2 D.1
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西省盟校高三第二次联考文科数学试卷(解析版) 题型:选择题
如图,直角梯形ABCD中, A=90°,
A=90°,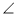 B=45°,底边AB=5,高AD=3,点E由B沿折线BCD向点D移动,EM
B=45°,底边AB=5,高AD=3,点E由B沿折线BCD向点D移动,EM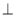 AB于M,EN
AB于M,EN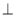 AD于N,设BM=
AD于N,设BM= ,矩形AMEN的面积为
,矩形AMEN的面积为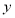 ,那么
,那么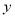 与
与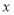 的函数关系的图像大致是( )
的函数关系的图像大致是( )
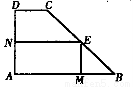
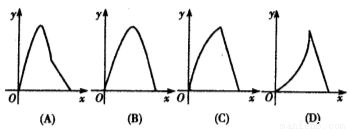
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西省盟校高三第一次联考文科数学试卷(解析版) 题型:填空题
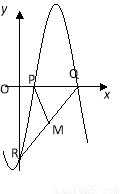
如图,函数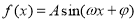 (其中
(其中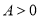 ,
,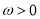 ,
,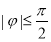 )与坐标轴的三个交点
)与坐标轴的三个交点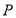 、
、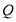 、
、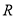 满足
满足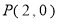 ,
,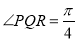 ,
,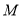 为
为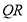 的中点,
的中点,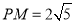 , 则
, 则 的值为____________
的值为____________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com