Question

【题目】已知函数f（x）=|x﹣a|﹣|x﹣2|．

（1）当a=﹣3时，求不等式f（x）＜2的解集；

（2）若x∈[1，2]时不等式f（x）＜2成立，求实数a的取值范围．

Answer 1

【答案】（1）不等式的解集为{x|x＜}；（2）实数a的取值范围是﹣2＜a＜4.

【解析】

（1）a=﹣3时，f（x）=|x+3|﹣|x﹣2|，零点分区间，去掉绝对值，分段解不等式即可；（2）原式等价于|x﹣a|＜2+|x﹣2|成立，即2x﹣4＜a＜4，而y=2x﹣4在[1，2]上的最小值为﹣2,进而得到参数范围.

（1）函数f（x）=|x﹣a|﹣|x﹣2|，

当a=﹣3时，f（x）=|x+3|﹣|x﹣2|=；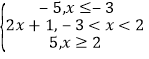

则x≤﹣3时，不等式f（x）＜2化为﹣5＜2，∴x≤﹣3；

﹣3＜x＜2时，不等式f（x）＜2化为2x+1＜2，∴﹣3＜x＜；

x≥2时，不等式f（x）＜2化为5＜2，∴x∈；

综上，不等式的解集为{x|x＜}；

（2）x∈[1，2]时不等式f（x）＜2成立，

即|x﹣a|﹣|x﹣2|＜2成立，

等价于|x﹣a|＜2+|x﹣2|成立；

∴|x﹣a|＜4﹣x，

∴x﹣4＜x﹣a＜4﹣x，

即2x﹣4＜a＜4；

又y=2x﹣4在[1，2]上的最小值为﹣2，

∴实数a的取值范围是﹣2＜a＜4．