设f（x）=
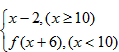
，则f（5）的值为
练习册系列答案
相关习题
科目：高中数学
来源：
题型：
设函数f（x）=a
2x
2（a＞0），g（x）=blnx．
（1）若函数y=f（x）图象上的点到直线x-y-3=0距离的最小值为
，求a的值；
（2）关于x的不等式（x-1）
2＞f（x）的解集中的整数恰有3个，求实数a的取值范围；
（3）对于函数f（x）与g（x）定义域上的任意实数x，若存在常数k，m，使得f（x）≥kx+m和g（x）≤kx+m都成立，则称直线y=kx+m为函数f（x）与g（x）的“分界线”．设
a=，b=e，试探究f（x）与g（x）是否存在“分界线”？若存在，求出“分界线”的方程；若不存在，请说明理由．
查看答案和解析>>
科目：高中数学
来源：
题型：
（2013•韶关一模）设f（x）在区间I上有定义，若对?x
1，x
2∈I，都有
f()≥，则称f（x）是区间I的向上凸函数；若对?x
1，x
2∈I，都有
f()≤，则称f（x）是区间I的向下凸函数，有下列四个判断：
①若f（x）是区间I的向上凸函数，则-f（x）在区间I的向下凸函数；
②若f（x）和g（x）都是区间I的向上凸函数，则f（x）+g（x）是区间I的向上凸函数；
③若f（x）在区间I的向下凸函数，且f（x）≠0，则
是区间I的向上凸函数；
④若f（x）是区间I的向上凸函数，?x
1，x
2，x
3，x
4∈I，则有f（
）≥
其中正确的结论个数是（ ）
查看答案和解析>>
科目：高中数学
来源：2011-2012学年浙江省台州市临海市杜桥中学高三（下）3月月考数学试卷（文科）（解析版）
题型：选择题
设f（x），g（x），h（x）是R上的任意实值函数，如下定义两个函数（f°g）（x）和（x）对任意x∈R，（f°g）（x）=f（g（x））；（x）=f（x）g（x），则下列等式恒成立的是（ ）
A．（（f°g）•h）（x）=°）（x）
B．°h）（x）=（（f°h）•（g°h））（x）
C．（（f°g）°h）（x）=（（f°h）°（g°h））（x）
D．•h）（x）=•）（x）
查看答案和解析>>
科目：高中数学
来源：2011-2012学年江西省重点中学协作体高三第一次联考数学试卷（理科）（解析版）
题型：选择题
设f（x），g（x），h（x）是R上的任意实值函数，如下定义两个函数（f°g）（x）和（x）对任意x∈R，（f°g）（x）=f（g（x））；（x）=f（x）g（x），则下列等式恒成立的是（ ）
A．（（f°g）•h）（x）=°）（x）
B．°h）（x）=（（f°h）•（g°h））（x）
C．（（f°g）°h）（x）=（（f°h）°（g°h））（x）
D．•h）（x）=•）（x）
查看答案和解析>>
科目：高中数学
来源：2011年广东省高考数学试卷（文科）（解析版）
题型：选择题
设f（x），g（x），h（x）是R上的任意实值函数，如下定义两个函数（f°g）（x）和（x）对任意x∈R，（f°g）（x）=f（g（x））；（x）=f（x）g（x），则下列等式恒成立的是（ ）
A．（（f°g）•h）（x）=°）（x）
B．°h）（x）=（（f°h）•（g°h））（x）
C．（（f°g）°h）（x）=（（f°h）°（g°h））（x）
D．•h）（x）=•）（x）
查看答案和解析>>
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
