解:(1)由

得

,
则

,任取

,
都有f(-x)=

=-f(x),则该函数为奇函数.
(2)任取0<x
1<x
2<1,
则有0<x
12<x
22<1?2-x
12>2-x
22>1,?ln(2-x
12)>ln(2-x
22)>0.
又

,
所以

,
即f(x
1)>f(x
2),
故函数f(x)在区间(0,1)上单调递减.
(3)由程序框图知,公差不为零的等差数列{a
n}要满足条件,
则必有f(a
1)+f(a
2)+…+f(a
10)=0.
由(1)知函数f(x)是奇函数,而奇函数的图象关于原点对称,
所以要构造满足条件的等差数列{a
n},可利用等差数列的性质,只需等差数列{a
n}
满足:a
1+a
10=a
2+a
9═a
5+a
6=0
且

即可.
我们可以先确定a
5,a
6使得a
5+a
6=0,因为公差不为零的等差数列{a
n}必是单调的数列,只要它的最大项和最小项在

中,即可满足要求.
所以只要a
5,a
6对应的点尽可能的接近原点.如取a
5=-0.1,a
6=0.1,存在满足条件的一个等差数列{a
n}可以是a
n=0.2n-1.1(1≤n≤10,n∈N
*).
分析:(1)先求出函数的定义域,得到定义域关于原点对称,在检验-x与x的函数值之间的关系,得到奇函数.
(2)根据单调性的定义,设出已知大小关系的任意两个变量,利用定义证明函数的单调性,得到函数是一个增函数.
(3)由程序框图知,公差不为零的等差数列{a
n}要满足条件,则必有f(a
1)+f(a
2)+…+f(a
10)=0.所以要构造满足条件的等差数列{a
n},可利用等差数列的性质,只需等差数列{a
n}满足:a
1+a
10=a
2+a
9═a
5+a
6=0.
点评:本题主要考查函数的奇偶性、单调性,以及借助于程序框图考查等差数列的有关性质,解题的关键是看清题目的实质,抓住解题的主要方法.

 (理)已知函数
(理)已知函数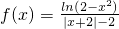 .
.
 ,
, ,任取
,任取  ,
, =-f(x),则该函数为奇函数.
=-f(x),则该函数为奇函数. ,
, ,
, 即可.
即可. 中,即可满足要求.
中,即可满足要求.

 名校课堂系列答案
名校课堂系列答案 ,其中
,其中 .
. ,使得
,使得 成立,求实数
成立,求实数 的取值范围;
的取值范围; 的值域.
的值域.