【答案】
分析:(1)由两向量的坐标,利用平面向量的数量积运算法则得到两向量和的坐标,再利用向量模的计算方法表示出两向量和的模,利用完全平方公式及同角三角函数间的基本关系化简后,根据已知两向量和的模得出sinα+cosα的值,两边平方后,再根据同角三角函数间的基本关系及二倍角的正弦函数公式即可求出sin2α的值;
(2)由
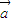
及
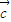
的坐标求出
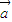
+
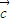
的坐标,再由
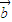
的坐标,利用平面向量的数量积运算法则计算所求的式子,配方后得到关于sinα的二次函数,配方后,根据正弦函数的值域得到自变量sinα的范围,利用二次函数的性质得到二次函数的值域即为所求式子的范围.
解答:解:(1)∵

+
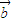
=(1+2cosα,1+2sinα),
|
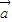
+
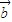
|=
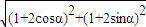
=

=
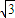
,
∴sinα+cosα=-

,
两边平方得:1+2sinαcosα=
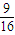
,
∴sin2α=-
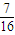
;
(2)因
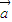
+
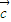
=(0,-1+sinα),
∴(
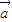
+
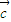
)•
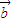
=sin
2α-sinα=
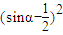
-

.
又sinα∈[-1,1],
∴(
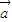
+
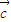
)•

的取值范围为[-

,2].
点评:此题考查了平面斜率的数量积运算法则,向量模的计算,同角三角函数间的基本关系,二倍角的正弦函数公式,正弦函数的值域以及二次函数的性质,熟练掌握法则、性质及公式是解本题的关键.

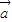 =(cosα,1+sinα),
=(cosα,1+sinα),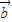 =(1+cosα,sinα).
=(1+cosα,sinα).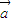 +
+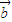 |=
|=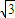 ,求sin2α的值;
,求sin2α的值;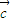 =(-cosα,-2),求(
=(-cosα,-2),求(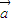 +
+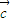 )•
)•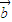 的取值范围.
的取值范围.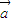 及
及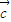 的坐标求出
的坐标求出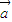 +
+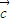 的坐标,再由
的坐标,再由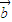 的坐标,利用平面向量的数量积运算法则计算所求的式子,配方后得到关于sinα的二次函数,配方后,根据正弦函数的值域得到自变量sinα的范围,利用二次函数的性质得到二次函数的值域即为所求式子的范围.
的坐标,利用平面向量的数量积运算法则计算所求的式子,配方后得到关于sinα的二次函数,配方后,根据正弦函数的值域得到自变量sinα的范围,利用二次函数的性质得到二次函数的值域即为所求式子的范围. +
+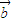 =(1+2cosα,1+2sinα),
=(1+2cosα,1+2sinα),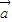 +
+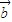 |=
|=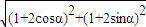
 =
=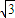 ,
, ,
,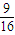 ,
,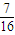 ;
;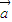 +
+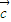 =(0,-1+sinα),
=(0,-1+sinα),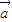 +
+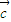 )•
)•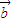 =sin2α-sinα=
=sin2α-sinα=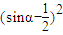 -
- .
.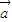 +
+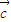 )•
)• 的取值范围为[-
的取值范围为[- ,2].
,2].

 优学名师名题系列答案
优学名师名题系列答案