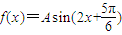练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知函数（A＞0，x∈R）的最小值为-2．
    （1）求f（0）；
    （2）若函数f（x）的图象向左平移ϕ（ϕ＞0）个单位长度，得到的曲线关于y轴对称，求ϕ的最小值．
    【答案】分析：（1）由函数的最值求出A，从而求得函数的解析式，进而求得f（0）的值．
    （2）函数f（x）的图象变换后得到的图象对应的函数解析式为，根据此曲线关于y轴对称，可得，由此求得ϕ的最小值．
    解答：解：（1）因为函数（A＞0，x∈R）的最小值为-2，
    所以A=2，…（2分），
    ．…（4分）
    （2）函数f（x）的图象向左平移ϕ（ϕ＞0）个单位长度，可得．…（6分）
    因为的图象关于y轴对称，所以．…（8分）
    解得，…（10分）
    因为ϕ＞0，所以ϕ的最小值为．…（12分）
    点评：本题主要考查由函数y=Asin（ωx+∅）的部分图象求解析式，函数y=Asin（ωx+∅）的图象变换规律以及对称性，属于中档题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    已知函数数学公式（A＞0，x∈R）的最小值为-2．
    （1）求f（0）；
    （2）若函数f（x）的图象向左平移?（?＞0）个单位长度，得到的曲线关于y轴对称，求?的最小值．

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年广东省揭阳三中高二（下）第一次段考数学试卷（理科）（解析版） 题型：解答题

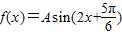    已知函数（A＞0，x∈R）的最小值为-2．
    （1）求f（0）；
    （2）若函数f（x）的图象向左平移ϕ（ϕ＞0）个单位长度，得到的曲线关于y轴对称，求ϕ的最小值．

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年山东省潍坊市三县市高一（上）期末数学试卷（解析版） 题型：填空题

    已知函数（a＞0，a≠1）的图象恒过定点A，若点A也在函数f（x）=3x+b的图象上，则b=    ．

    查看答案和解析>>

    科目：高中数学 来源：2012年全国普通高等学校招生统一考试文科数学（天津卷解析版） 题型：解答题

    已知函数其中a>0.

    （I）求函数f(x)的单调区间；

    （II）若函数f（x）在区间（-2，0）内恰有两个零点，求a的取值范围；

    （III）当a=1时，设函数f（x）在区间[t,t+3]上的最大值为M（t），最小值为m（t）,记g(t)=M(t)-m(t),求函数g(t)在区间[-3，-1]上的最小值。

    【考点定位】本小题主要考查导数的运算，利用导数研究函数的单调性、函数的零点，函数的最值等基础知识.考查函数思想、分类讨论思想.考查综合分析和解决问题的能力.

     

    查看答案和解析>>

    同步练习册答案