解:(1)设f(x)图象上任一点坐标为(x,y),
点(x,y)关于点A(0,1)的对称点(-x,2-y)在h(x)的图象上(3分)
∴
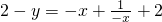
,
∴
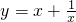
,即

(6分)
f(x)的定义域为:{x|x≠0),值域为:{x|x≤0或x≥4}
(2)由题意
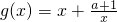
,且
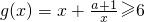
∵x∈(0,2]
∴a+1≥x(6-x),即a≥-x
2+6x-1,(9分)
令q(x)=-x
2+6x-1,x∈(0,2],q(x)=-x
2+6x-1=-(x-3)
2+8,
∴x∈(0,2]时,q(x)
max=7(11分)
∴a≥7(13分)
方法二:q′(x)=-2x+6,x∈(0,2]时,q′(x)>0
即q(x)在(0,2]上递增,
∴x∈(0,2]时,q(x)
max=7
即 a≥x
2-1在x∈(0,2]时恒成立.
∵x∈(0,2]时,(x
2-1)
max=3
∴a≥3
∴a≥7
分析:(1)主要是利用中点坐标公式得出对称点的坐标,然后代入函数表达式就可求出函数解析式,再根据解析式写出定义域和值域.
(2)因为在这个区间上x>0,所以可以分离常数法讲参数a和自变量x分到不等式的两边,问题就转化为求关于x的一个函数在这个区间上的求最值问题,法一:是利用二此函数的配方法求出函数在这个区间上的最大值;法二:是利用导数法求出函数在这个区间上的最大值,求出最大值后从而就可以求出a的取值范围.
点评:本题第1问主要考查函数关于点对称的问题,主要用中点坐标公式解决,第2问考查恒成立问题,此类问题经常先分离常数,在转化为函数求最值问题.

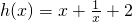 的图象关于点A(0,1)对称.
的图象关于点A(0,1)对称. ,且g(x)在区间(0,2]上的值不小于6,求实数a的取值范围.
,且g(x)在区间(0,2]上的值不小于6,求实数a的取值范围.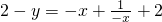 ,
,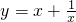 ,即
,即 (6分)
(6分)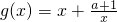 ,且
,且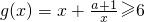


 高效智能课时作业系列答案
高效智能课时作业系列答案