
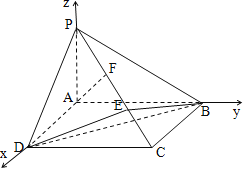
【题目】已知如图所示,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E、F分别为PC的三等分点.
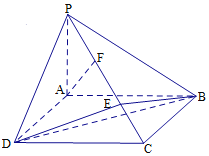
(1)证明:AF∥平面EBD;
(2)已知AP=AD=1,AB=2,求二面角E-BD-A的余弦值.
【答案】(1)见解析;(2)![]()
【解析】
(1)连接AC交于BD点O,连接EO,由E、F分别为PC的三等分点,得到AF∥EO,利用线面平行的判定定理,即可证得AF∥平面EBD.
(2)以A为原点,AD、AB、AP的分别为x,y,z轴方向建立空间直角坐标系,求得平面![]() 和平面
和平面![]() 的法向量,利用向量的夹角公式,即可求解.
的法向量,利用向量的夹角公式,即可求解.
(1)连接AC交于BD点O,连接EO.因为ABCD为矩形,
所以O为AC的中点.又E、F分别为PC的三等分点,
E为CF的中点,所以AF∥EO.
因为EO平面BDE,AF平面BDE,所以AF∥平面EBD.
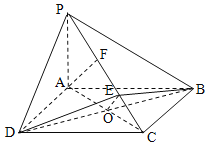
(2)以A为原点,AD、AB、AP的分别为x,y,z轴方向建立空间直角坐标系,
如图所示由条件可得D(1,0,0),B(0,2,0),C(1,2,0),P(0,0,1),
∵![]() ,∴
,∴![]() ,
,
![]() ,
,![]() 为平面ABD的一个法向量,
为平面ABD的一个法向量,
设面BDE的一个法向量为![]() ,则
,则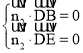 ,即
,即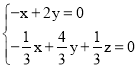 ,
,
取y=1,则x=2,z=-2,所以![]() ,
,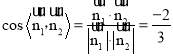 ,
,
所以二面角D-AE-C的余弦值为![]() .
.


 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源: 题型:
【题目】《流浪地球》是由刘慈欣的科幻小说改编的电影,在2019年春节档上影,该片上影标志着中国电影科幻元年的到来;为了振救地球,延续百代子孙生存的希望,无数的人前仆后继,奋不顾身的精神激荡人心,催人奋进.某网络调查机构调查了大量观众的评分,得到如下统计表:

(1)求观众评分的平均数?
(2)视频率为概率,若在评分大于等于8分的观众中随机地抽取1人,他的评分恰好是10分的概率是多少?
(3)视频率为概率,在评分大于等于8分的观众中随机地抽取4人,用![]() 表示评分为10分的人数,求
表示评分为10分的人数,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】重庆一中将要举行校园歌手大赛,现有3男3女参加,需要安排他们的出场顺序.(结果用数字作答)
(1)如果3个女生都不相邻,那么有多少种不同的出场顺序?
(2)如果女生甲在女生乙的前面(可以不相邻),那么有多少种不同的出场顺序?
(3)如果3位男生都相邻,且女生甲不在第一个出场,那么有多少种不同的出场顺序?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 1(a>b>0),椭圆C上的点到焦点距离的最大值为9,最小值为1.
1(a>b>0),椭圆C上的点到焦点距离的最大值为9,最小值为1.
(1)求椭圆C的标准方程;
(2)求椭圆C上的点到直线l:4x﹣5y+40=0的最小距离?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex-m(x+1)+1(m∈R).
(1)若函数f(x)的极小值为1,求实数m的值;
(2)当x≥0时,不等式![]() 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列1,1,2,1,2,4,1,2,4,8,1,2,4,8,16,![]() 其中第一项是
其中第一项是![]() ,接下来的两项是
,接下来的两项是![]() ,
,![]() ,再接下来的三项是
,再接下来的三项是![]() ,
,![]() ,
,![]() ,依此类推那么该数列的前50项和为
,依此类推那么该数列的前50项和为![]()
![]()
A. 1044 B. 1024 C. 1045 D. 1025
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,四边形ABCD是菱形,![]() ,BD=2.
,BD=2.
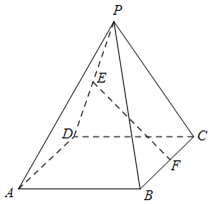
(1)若点E,F分别为线段PD,BC上的中点,求证:EF∥平面PAB;
(2)若平面PBD⊥平面ABCD,且PD⊥PB,PD=PB,求平面PAB与平面PBC所成的锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
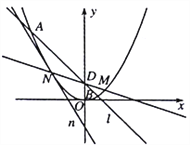
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() 在抛物线
在抛物线![]() :
: ![]() 上,直线
上,直线![]() :
: ![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
, ![]() 两点,且直线
两点,且直线![]() ,
, ![]() 的斜率之和为-1.
的斜率之和为-1.
(1)求![]() 和
和![]() 的值;
的值;
(2)若![]() ,设直线
,设直线![]() 与
与![]() 轴交于
轴交于![]() 点,延长
点,延长![]() 与抛物线
与抛物线![]() 交于点
交于点![]() ,抛物线
,抛物线![]() 在点
在点![]() 处的切线为
处的切线为![]() ,记直线
,记直线![]() ,
, ![]() 与
与![]() 轴围成的三角形面积为
轴围成的三角形面积为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com