
 如图,设P(x1,y1),Q(x2,y2)是抛物线C:y2=2px(p>0)上相异两点,且
如图,设P(x1,y1),Q(x2,y2)是抛物线C:y2=2px(p>0)上相异两点,且 ,直线QP与x轴相交于E.
,直线QP与x轴相交于E.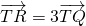 ,若存在,求出F点的坐标(用p表示),若不存在,说明理由.
,若存在,求出F点的坐标(用p表示),若不存在,说明理由. ,则x1x2+y1y2=0,
,则x1x2+y1y2=0,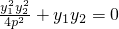 ,
,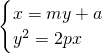 ,
,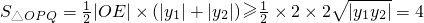 ,∴面积最小值为4.…(6分)
,∴面积最小值为4.…(6分)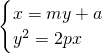 ,
,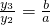 ③
③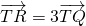 ,设T(c,0),则有(x3-c,y3-0)=3(x2-c,y2-0),∴y3=3y2即
,设T(c,0),则有(x3-c,y3-0)=3(x2-c,y2-0),∴y3=3y2即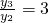 ④
④ ,y1y2=-4p2,代入①,
,y1y2=-4p2,代入①,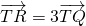 .…(12分)
.…(12分) ,知x1x2+y1y2=0,由P、Q在抛物线上,得
,知x1x2+y1y2=0,由P、Q在抛物线上,得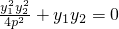 ,y1y2=-4p2?|y1y2|=4p2,又|y1y2|=4,故得y2=2x,设E(a,0)(a≠0),直线PQ方程为x=my+a,联立方程
,y1y2=-4p2?|y1y2|=4p2,又|y1y2|=4,故得y2=2x,设E(a,0)(a≠0),直线PQ方程为x=my+a,联立方程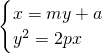 ,得y2-2pmy-2pa=0.由此能导出该抛物线方程及△OPQ的面积的最小值.
,得y2-2pmy-2pa=0.由此能导出该抛物线方程及△OPQ的面积的最小值.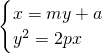 ,得y2-2pmy-2pa=0,由此能导出在x轴上,存在异于E的一点F(6p,0),使得
,得y2-2pmy-2pa=0,由此能导出在x轴上,存在异于E的一点F(6p,0),使得 .
.

 黄冈创优卷系列答案
黄冈创优卷系列答案科目:高中数学 来源: 题型:
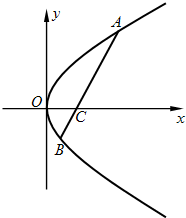 在平面直角坐标系xOy中,过定点C(p,0)作直线与抛物线y2=2px(p>0)相交于A,B两点,如图,设动点A(x1,y1)、B(x2,y2).
在平面直角坐标系xOy中,过定点C(p,0)作直线与抛物线y2=2px(p>0)相交于A,B两点,如图,设动点A(x1,y1)、B(x2,y2).查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•虹口区一模)已知圆O:x2+y2=4.
(2013•虹口区一模)已知圆O:x2+y2=4.| 3 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
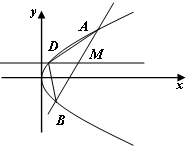 已知抛物线C:y2=2px(p>0)上有一点Q(2,y0)到焦点F的距离为
已知抛物线C:y2=2px(p>0)上有一点Q(2,y0)到焦点F的距离为| 5 | 2 |
查看答案和解析>>
科目:高中数学 来源:2009-2010学年山东省青岛市平度一中高二(上)第二次段考数学试卷(理科)(解析版) 题型:解答题
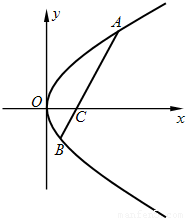
查看答案和解析>>
科目:高中数学 来源:2013年上海市虹口区高考数学一模试卷(文理合卷)(解析版) 题型:解答题
 与圆O相交于A、B两点,求|AB|;
与圆O相交于A、B两点,求|AB|;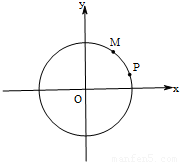
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com