分析:①由题意可得A1N∥BM,由线面平行的判定定理可得:A1N∥平面BMC1.同理可得:CN∥平面BMC1.再结合面面平行的判定定理可得面面平行.
②根据A1N∥BM,并且AC∥A1C1,可得BM与AC所成角等于A1C1与A1N所成的角,即∠NA1C1为所求或者与其互补.然后把角放入三角形中利用解三角形的有关知识解决问题即可.
解答:解:①证明:在正三棱柱ABC-A
1B
1C
1中,M、N分别为A
1B
1、AB的中点,
所以A
1N∥BM,
因为BM?平面BMC
1,A1N?平面BMC
1,
所以A
1N∥平面BMC
1.
因为M、N分别为A
1B
1、AB的中点,
所以C1M∥CN,
因为C1M?平面BMC
1,CN?平面BMC
1,
所以CN∥平面BMC
1.
又因为CN∩A
1N=N,并且CN?平面A
1NC,A
1N?平面A
1NC
所以平面A
1NC∥平面BMC
1.
②由 ①可得A
1N∥BM,
又因为AC∥A
1C
1,
所以BM与AC所成角等于A
1C
1与A
1N所成的角,
即∠NA
1C
1为所求或者与其互补.
连接C
1N,在△NA
1C
1中,设AB=AA
1=2,所以A
1N=
,A
1C
1=2,NC
1=
,
所以根据余弦定理可得:cosNA
1C
1=
.
所以BM与AC所成角的余弦值
.
点评:解决此类问题的关键是熟练掌握几何体的结构特征,进而得到线面关系与面面关系,以及熟练掌握空间角的求法(步骤是先作角,再证角,然后放入三角形进行求解).

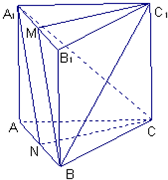 正三棱柱ABC-A1B1C1中,M、N分别为A1B1、AB的中点.
正三棱柱ABC-A1B1C1中,M、N分别为A1B1、AB的中点.

 如图:在正三棱柱ABC-A1 B1 C1中,AB=
如图:在正三棱柱ABC-A1 B1 C1中,AB= 如图在 正三棱柱ABC-A1 B1 C1中,底面边长为
如图在 正三棱柱ABC-A1 B1 C1中,底面边长为 如图,在正三棱柱ABC-A1 B1 C1中,AA1=4,AB=2,M是AC的中点,点N在AA1上,AN=
如图,在正三棱柱ABC-A1 B1 C1中,AA1=4,AB=2,M是AC的中点,点N在AA1上,AN= 如图:在正三棱柱ABC-A1 B1 C1中,AB=
如图:在正三棱柱ABC-A1 B1 C1中,AB= =a,E,F分别是BB1,CC1上的点且BE=a,CF=2a.
=a,E,F分别是BB1,CC1上的点且BE=a,CF=2a. =a,E,F分别是BB1,CC1上的点且BE=a,CF=2a.
=a,E,F分别是BB1,CC1上的点且BE=a,CF=2a.