
已知点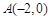 ,
,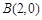 ,直线AG,BG相交于点G,且它们的斜率之积是
,直线AG,BG相交于点G,且它们的斜率之积是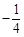 .
.
(Ⅰ)求点G的轨迹 的方程;
的方程;
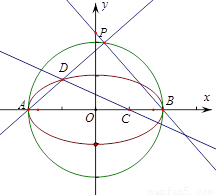
(Ⅱ)圆 上有一个动点P,且P在x轴的上方,点
上有一个动点P,且P在x轴的上方,点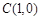 ,直线PA交(Ⅰ)中的轨迹
,直线PA交(Ⅰ)中的轨迹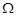 于D,连接PB,CD.设直线PB,CD的斜率存在且分别为
于D,连接PB,CD.设直线PB,CD的斜率存在且分别为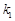 ,
,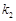 ,若
,若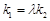 ,求实数
,求实数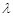 的取值范围.
的取值范围.
(Ⅰ)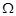 的方程是
的方程是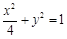 (
(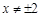 );(Ⅱ)
);(Ⅱ) .
.
【解析】
试题分析:(Ⅰ)设 ,代入
,代入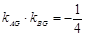 即得
即得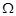 的轨迹方程:
的轨迹方程: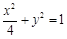 ;(Ⅱ)注意,AB是圆
;(Ⅱ)注意,AB是圆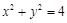 的直径,所以直线
的直径,所以直线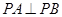 ,
,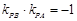 ,即
,即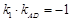 .因为
.因为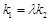 ,所以
,所以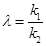 .为了求
.为了求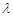 的取值范围,我们将
的取值范围,我们将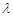 用某个变量表示出来.为此,设
用某个变量表示出来.为此,设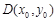 ,∵动点
,∵动点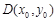 在圆
在圆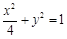 上,所以
上,所以 ,这样得一
,这样得一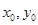 间的关系式.我们可以将
间的关系式.我们可以将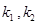 都用
都用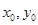 表示出来,然后利用
表示出来,然后利用 将
将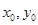 换掉一个,这样就可得
换掉一个,这样就可得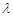 的取值范围.这里为什么不设
的取值范围.这里为什么不设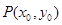 ,请读者悟一悟其中的奥妙
,请读者悟一悟其中的奥妙
试题解析:(Ⅰ)设 ,由
,由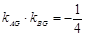 得,
得, (
(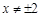 ), 3分
), 3分
化简得动点G的轨迹 的方程为
的方程为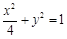 (
(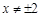 ). 6分
). 6分
(未注明条件“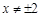 ”扣1分)
”扣1分)
(Ⅱ)设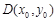 ,∵动点P在圆
,∵动点P在圆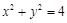 上,∴
上,∴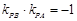 ,即
,即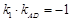 ,
,
∴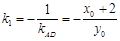 ,又
,又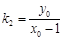 (
(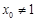 ), 8分
), 8分
由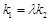 ,得
,得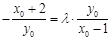 ,
,
∴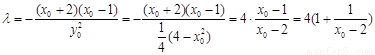 , 10分
, 10分
由于 且
且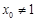 , 11分
, 11分
解得 . 13分
. 13分
考点:1、椭圆及圆的方程的方程;2、直线与圆锥曲线的关系;3、范围问题.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•长春一模)请考生在22、23、24三题中任选一题作答,如果多做,则按所做的第一题记分.
(2013•长春一模)请考生在22、23、24三题中任选一题作答,如果多做,则按所做的第一题记分. |
| BD |
| GF |
| AG |
| EF2 |
| CE2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x |
| f(x)-ag(x) |
| f(x) |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com