
分析 ( I)由已知等式及三角形面积公式,可得:$tanC=\sqrt{3}$,结合范围C∈(0,$\frac{π}{2}$),即可得解C的值.
( II)由正弦定理得$a=\frac{4}{3}\sqrt{3}{sinA}$,$b=\frac{4}{3}\sqrt{3}sinB$,利用三角函数恒等变换的应用可得a+b=4sin(A+$\frac{π}{6}$),由范围$0<A<\frac{2π}{3}$,可求A+$\frac{π}{6}$的范围,利用正弦函数的性质可求其取值范围.
解答 (本小题满分12分)
解:( I)由已知:$S=\frac{{\sqrt{3}}}{2}abcosC$.
由三角形面积公式:$S=\frac{1}{2}absinC$
联立可得:$tanC=\sqrt{3}$,且C∈(0,$\frac{π}{2}$),可得:C=$\frac{π}{3}$,
所以,角C的值为$\frac{π}{3}$…(6分)
( II)因为A为三角形内角,所以$0<A<\frac{2π}{3}$,
由正弦定理得:$a=\frac{4}{3}\sqrt{3}{sinA}$,$b=\frac{4}{3}\sqrt{3}sinB$,…(7分)
$\begin{array}{l}a+b=\frac{{4\sqrt{3}}}{3}{sinA}+\frac{{4\sqrt{3}}}{3}{sinB}=\frac{{4\sqrt{3}}}{3}{sinA}+\frac{{4\sqrt{3}}}{3}sin(\frac{2π}{3}-A)\\=4sin(A+\frac{π}{6})\end{array}$…(9分)
∵$A∈(0,\frac{2π}{3})$,
∴$sin(A+\frac{π}{6})∈(\frac{1}{2},1]$,
∴a+b∈(2,4],
所以b+c的取值范围为(2,4].…(12分)
点评 本题主要考查了三角形面积公式,正弦定理,三角函数恒等变换的应用,正弦函数的图象和性质在解三角形中的应用,考查了计算能力和转化思想,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
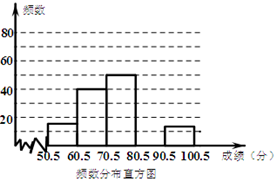 2013年3月28日是全国中小学生安全教育日,某学校为加强学生的安全意识,组织了全校1500名学生参加安全知识竞赛,从中抽取了部分学生成绩进行统计.请根据尚未完成的频率分布表和频数分布直方图,解答下列问题:
2013年3月28日是全国中小学生安全教育日,某学校为加强学生的安全意识,组织了全校1500名学生参加安全知识竞赛,从中抽取了部分学生成绩进行统计.请根据尚未完成的频率分布表和频数分布直方图,解答下列问题:| 分数段 | 频数 | 频率 |
| 50.5~60.5 | 16 | 0.08 |
| 60.5~70.5 | 40 | 0.2 |
| 70.5~80.5 | 50 | 0.25 |
| 80.5~90.5 | m | 0.35 |
| 90.5~100.5 | 24 | n |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com