
| A. | (0,$\frac{1}{e}$) | B. | (0,$\frac{1}{2e}$) | C. | [$\frac{ln3}{3}$,$\frac{1}{2e}$] | D. | [$\frac{ln3}{3}$,$\frac{1}{e}$) |
分析 由g(x)=|f(x)|-kx-k=0得|f(x)|=kx+k,设y=kx+k=k(x+1),作出两个函数的图象,利用数形结合,结合函数的切线关系进行求解即可.
解答 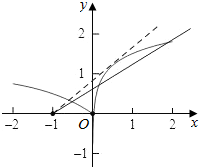 解:由g(x)=|f(x)|-kx-k=0得|f(x)|=kx+k,
解:由g(x)=|f(x)|-kx-k=0得|f(x)|=kx+k,
设y=kx+k=k(x+1),则直线过定点(-1,0),
作出函数|f(x)|的图象如图:
当k≤0时,不满足条件.
当k>0时,当直线设y=kx+k=k(x+1)经过点(2,ln3)时,此时两个函数有3个交点,
此时3k=ln3,则k=$\frac{ln3}{3}$,
当直线y=kx+k=k(x+1)与y=ln(x+1)相切时,有两个交点,
此时函数的导数f′(x)=$\frac{1}{x+1}$,
设切点坐标为(a,b),则b=ln(a+1),切线斜率为f′(a)=$\frac{1}{a+1}$,
则切线方程为y-ln(a+1)=$\frac{1}{a+1}$(x-a),
即y=$\frac{1}{a+1}$(x-a)+ln(a+1)=$\frac{1}{a+1}$•x-$\frac{a}{a+1}$+ln(a+1)
∵y=kx+k,
∴k=$\frac{1}{a+1}$•且k=-$\frac{a}{a+1}$+ln(a+1)
即$\frac{1}{a+1}$=-$\frac{a}{a+1}$+ln(a+1),
即$\frac{1}{a+1}$+$\frac{a}{a+1}$=ln(a+1)=1,
则a+1=e,即a=e-1,
则k=$\frac{1}{a+1}$=$\frac{1}{e}$,
∴要使两个函数有3个交点,则$\frac{ln3}{3}$≤k<$\frac{1}{e}$,
故选:D
点评 本题主要考查函数零点个数的判断,根据函数与方程之间的关系转化为两个函数的交点个数问题是解决本题的关键.注意要利用数形结合.


科目:高中数学 来源: 题型:选择题
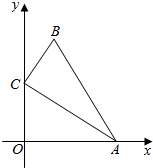 如图,在△ABC中,∠ACB=90°,AC=2,BC=1,点A、C分别在x轴、y轴上,当点A在x轴上运动时,点C随之在y轴上运动,在运动过程中,点B到原点O的最大距离是( )
如图,在△ABC中,∠ACB=90°,AC=2,BC=1,点A、C分别在x轴、y轴上,当点A在x轴上运动时,点C随之在y轴上运动,在运动过程中,点B到原点O的最大距离是( )| A. | 3 | B. | $\sqrt{6}$ | C. | $1+\sqrt{2}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
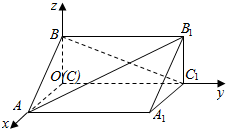 如图,在空间直角坐标系中有直三棱柱ABC-A1B1C1,CA=2CB,CC1=3CB,则直线BC1与直线AB1夹角的余弦值为( )
如图,在空间直角坐标系中有直三棱柱ABC-A1B1C1,CA=2CB,CC1=3CB,则直线BC1与直线AB1夹角的余弦值为( )| A. | $\frac{4\sqrt{35}}{35}$ | B. | $\frac{\sqrt{35}}{70}$ | C. | $\frac{2\sqrt{35}}{35}$ | D. | $\frac{2}{35}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 无数个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
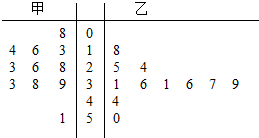 如图是甲、乙两名篮球运动员某赛季一些场次得分的茎叶图,其中茎为十位数,叶为个位数,甲、乙两人得分的中位数为X甲、X乙,则下列判断正确的是( )
如图是甲、乙两名篮球运动员某赛季一些场次得分的茎叶图,其中茎为十位数,叶为个位数,甲、乙两人得分的中位数为X甲、X乙,则下列判断正确的是( )| A. | X乙-X甲=5,甲比乙得分稳定 | B. | X乙-X甲=5,乙比甲得分稳定 | ||
| C. | X乙-X甲=10,甲比乙得分稳定 | D. | X乙-X甲=10,乙比甲得分稳定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com