
| A. | 0 | B. | 1 | C. | 2 | D. | 无数个 |
分析 以A为坐标原点建立如图所示的空间坐标系,利用向量垂直的充要条件,判断满足条件的点E的个数,进而得到答案.
解答 解:以A为坐标原点建立如图所示的空间坐标系,
则D(0,2,0),D1(0,2,3),
设A1E=λA1C,(0≤λ≤1),
则由A1(0,0,3),$\overrightarrow{{A}_{1}C}$=(1,2,-3)得:
$\overrightarrow{AE}$=(λ,2λ,3-3λ),
则$\overrightarrow{ED}$=(-λ,2-2λ,3λ-3),$\overrightarrow{{ED}_{1}}$=(-λ,2-2λ,3λ),
若ED⊥ED1,则$\overrightarrow{ED}$⊥$\overrightarrow{{ED}_{1}}$,
即λ2+(2-2λ)2+3λ(3λ-3)=0,
即14λ2-17λ+4=0,
解得:λ=$\frac{17±\sqrt{65}}{28}$,
故存在两个满足条件的点,
故选:C.
点评 本题考查的知识点是空间中直线与直线之间的位置关系,向量垂直的充要条件,难度中档.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:填空题
 如图是用条件语句编写的一个程序:若输入4,则输出的结果是15,该程序的功能是求函数$y=\left\{{\begin{array}{l}{{x^2}-1}\\ 2\\{2x}\end{array}}\right.,\begin{array}{l}{x>3}\\{x=3}\\{x<3}\end{array}$的值.
如图是用条件语句编写的一个程序:若输入4,则输出的结果是15,该程序的功能是求函数$y=\left\{{\begin{array}{l}{{x^2}-1}\\ 2\\{2x}\end{array}}\right.,\begin{array}{l}{x>3}\\{x=3}\\{x<3}\end{array}$的值.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p1,p4 | B. | p1p2 | C. | p2,p4 | D. | p3,p4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{e}$) | B. | (0,$\frac{1}{2e}$) | C. | [$\frac{ln3}{3}$,$\frac{1}{2e}$] | D. | [$\frac{ln3}{3}$,$\frac{1}{e}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
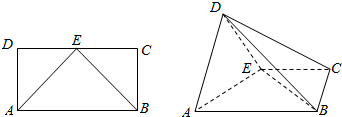 如图,在长方形ABCD中,AB=2,AD=1,E为CD的中点,以AE为折痕,把△DAE折起为△D′AE,且平面D′AE⊥平面ABCE.
如图,在长方形ABCD中,AB=2,AD=1,E为CD的中点,以AE为折痕,把△DAE折起为△D′AE,且平面D′AE⊥平面ABCE.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | ¬p∧q | C. | p∧¬q | D. | ¬p∧¬q |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com