
【题目】已知a∈R,若 ![]() 在区间(0,1)上只有一个极值点,则a的取值范围为 .
在区间(0,1)上只有一个极值点,则a的取值范围为 .
【答案】a>0
【解析】解:∵f(x)=(x+ ![]() )ex , ∴f′(x)=(
)ex , ∴f′(x)=( ![]() )ex ,
)ex ,
设h(x)=x3+x2+ax﹣a,
∴h′(x)=3x2+2x+a,
a>0,h′(x)>0在(0,1)上恒成立,即函数h(x)在(0,1)上为增函数,
∵h(0)=﹣a<0,h(1)=2>0,
∴h(x)在(0,1)上有且只有一个零点x0 , 使得f′(x0)=0,
且在(0,x0)上,f′(x)<0,在(x0 , 1)上,f′(x)>0,
∴x0为函数f(x)在(0,1)上唯一的极小值点;
a=0时,x∈(0,1),h′(x)=3x2+2x>0成立,函数h(x)在(0,1)上为增函数,
此时h(0)=0,∴h(x)>0在(0,1)上恒成立,
即f′(x)>0,函数f(x)在(0,1)上为单调增函数,函数f(x)在(0,1)上无极值;
a<0时,h(x)=x3+x2+a(x﹣1),
∵x∈(0,1),∴h(x)>0在(0,1)上恒成立,
即f′(x)>0,函数f(x)在(0,1)上为单调增函数,函数f(x)在(0,1)上无极值.
综上所述,a>0,所以答案是:a>0.
【考点精析】解答此题的关键在于理解函数的极值与导数的相关知识,掌握求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
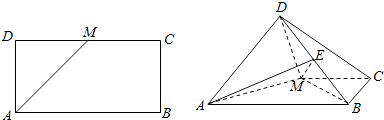
【题目】如图,已知长方形ABCD中,AB=2 ![]() ,AD=
,AD= ![]() ,M为DC的中点,将△ADM沿AM折起,使得平面ADM⊥平面ABCM (Ⅰ)求证:AD⊥BM
,M为DC的中点,将△ADM沿AM折起,使得平面ADM⊥平面ABCM (Ⅰ)求证:AD⊥BM
(Ⅱ)若点E是线段DB上的一动点,问点E在何位置时,二面角E﹣AM﹣D的余弦值为 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,平面ABCD⊥平面ABEF,四边形ABCD是正方形,四边形ABEF是矩形,且AF= ![]() AD=a,G是EF的中点,则GB与平面AGC所成角的正弦值为( )
AD=a,G是EF的中点,则GB与平面AGC所成角的正弦值为( ) 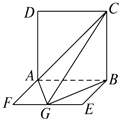
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知隧道的截面是半径为4.0 m的半圆,车辆只能在道路中心线一侧行驶,一辆宽为2.7 m,高为3 m的货车能不能驶入这个隧道?假设货车的最大宽度为a m,那么要正常驶入该隧道,货车的限高为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】到直线3x-4y+1=0的距离为3,且与此直线平行的直线方程是 ( )
A.3x-4y+4=0
B.3x-4y+4=0或3x-4y-2=0
C.3x-4y+16=0
D.3x-4y+16=0或3x-4y-14=0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com