
【题目】已知![]() ,
,![]() ,动点
,动点![]() 满足直线
满足直线![]() 与直线
与直线![]() 的斜率之积为
的斜率之积为![]() ,设点
,设点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)若过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,过点
两点,过点![]() 且与直线
且与直线![]() 垂直的直线与
垂直的直线与![]() 相交于点
相交于点![]() ,求
,求![]() 的最小值及此时直线
的最小值及此时直线![]() 的方程.
的方程.
【答案】(1)![]() (2)
(2)![]() 的最小值为1,此时直线
的最小值为1,此时直线![]() :
:![]()
【解析】
(1)用直接法求轨迹方程,即设动点为![]() ,把已知用坐标表示并整理即得.注意取值范围;
,把已知用坐标表示并整理即得.注意取值范围;
(2)设![]() :
:![]() ,将其与曲线
,将其与曲线![]() 的方程联立,消元并整理得
的方程联立,消元并整理得![]() ,
,
设![]() ,
,![]() ,则可得
,则可得![]() ,
,![]() ,由
,由![]() 求出
求出![]() ,
,
将直线![]() 方程
方程![]() 与
与![]() 联立,得
联立,得![]() ,求得
,求得![]() ,计算
,计算![]() ,设
,设![]() .显然
.显然![]() ,构造
,构造![]() ,由导数的知识求得其最小值,同时可得直线
,由导数的知识求得其最小值,同时可得直线![]() 的方程.
的方程.
(1)设![]() ,则
,则![]() ,即
,即![]()
整理得![]()
(2)设![]() :
:![]() ,将其与曲线
,将其与曲线![]() 的方程联立,得
的方程联立,得![]()
即![]()
设![]() ,
,![]() ,则
,则![]() ,
,![]()
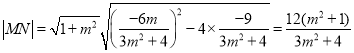
将直线![]() :
:![]() 与
与![]() 联立,得
联立,得![]()
∴![]()
∴
设![]() .显然
.显然![]()
构造![]()
![]() 在
在![]() 上恒成立
上恒成立
所以![]() 在
在![]() 上单调递增
上单调递增
所以![]() ,当且仅当
,当且仅当![]() ,即
,即![]() 时取“=”
时取“=”
即![]() 的最小值为1,此时直线
的最小值为1,此时直线![]() :
:![]() .
.
(注:1.如果按函数![]() 的性质求最值可以不扣分;2.若直线方程按斜率是否存在讨论,则可以根据步骤相应给分.)
的性质求最值可以不扣分;2.若直线方程按斜率是否存在讨论,则可以根据步骤相应给分.)


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】对于数列![]() ,若从第二项起的每一项均大于该项之前的所有项的和,则称
,若从第二项起的每一项均大于该项之前的所有项的和,则称![]() 为
为![]() 数列.
数列.
(1)若![]() 的前
的前![]() 项和
项和![]() ,试判断
,试判断![]() 是否是
是否是![]() 数列,并说明理由;
数列,并说明理由;
(2)设数列![]() 是首项为
是首项为![]() 、公差为
、公差为![]() 的等差数列,若该数列是
的等差数列,若该数列是![]() 数列,求
数列,求![]() 的取值范围;
的取值范围;
(3)设无穷数列![]() 是首项为
是首项为![]() 、公比为
、公比为![]() 的等比数列,有穷数列
的等比数列,有穷数列![]() ,
,![]() 是从
是从![]() 中取出部分项按原来的顺序所组成的不同数列,其所有项和分别为
中取出部分项按原来的顺序所组成的不同数列,其所有项和分别为![]() ,
,![]() ,求
,求![]() 是
是![]() 数列时
数列时![]() 与
与![]() 所满足的条件,并证明命题“若
所满足的条件,并证明命题“若![]() 且
且![]() ,则
,则![]() 不是
不是![]() 数列”.
数列”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,离心率为
,离心率为![]() ,
,![]() 为椭圆上一动点(异于左右顶点),
为椭圆上一动点(异于左右顶点),![]() 面积的最大值为
面积的最大值为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与椭圆
与椭圆![]() 相交于点
相交于点![]() 两点,问
两点,问![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 是以
是以![]() 为直角顶点的等腰直角三角形?若存在,求点
为直角顶点的等腰直角三角形?若存在,求点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,某游乐园的一个摩天轮半径为10米,轮子的底部在地面上2米处,如果此摩天轮每20分钟转一圈,当摩天轮上某人经过![]() 处时开始计时(按逆时针方向转),
处时开始计时(按逆时针方向转),![]() (其中
(其中![]() 平行于地面).
平行于地面).
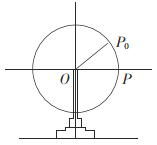
(1)求开始转动5分钟时此人相对于地面的高度.
(2)开始转动![]() 分钟时,摩天轮上此人经过点
分钟时,摩天轮上此人经过点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点![]() 且椭圆的短轴长为
且椭圆的短轴长为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)已知动直线![]() 过右焦点
过右焦点![]() ,且与椭圆
,且与椭圆![]() 分别交于
分别交于![]() 两点.试问
两点.试问![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得,
,使得,![]() 恒成立?若存在求出点
恒成立?若存在求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】政府为了对过热的房地产市场进行调控决策,统计部门对城市人和农村人进行了买房的心理预期调研,用简单随机抽样的方法抽取110人进行统计,得到如图列联表,已知样本中城市人数与农村人数之比是![]() ;
;
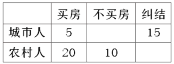
(Ⅰ)分别求样本中城市人中的不买房人数和农村人中的纠结人数;
(Ⅱ)请完成列联表,并用独立性检验的思想方法说明有多少的把握认为不买房心理预期与城乡有关?
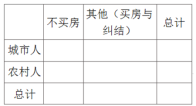
参考公式: ,
,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】棉花的纤维长度是棉花质量的重要指标.在一批棉花中抽测了60根棉花的纤维长度(单位:![]() ),将样本数据制作成如下的频率分布直方图:
),将样本数据制作成如下的频率分布直方图:
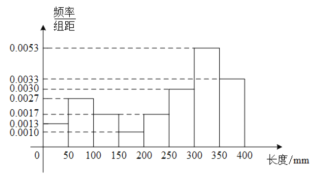
下列关于这批棉花质量状况的分析不正确的是( )
A.纤维长度在![]() 的棉花的数量为9根
的棉花的数量为9根
B.从这60根棉花中随机选取1根,其纤维长度在![]() 的概率为0.335
的概率为0.335
C.有超过一半的棉花纤维长度能达到![]() 以上
以上
D.这批棉花的纤维长度的中位数的估计值为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的右焦点为
的右焦点为![]() ,短轴长为2,过定点
,短轴长为2,过定点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于不同的两点
于不同的两点![]() 、
、![]() (点
(点![]() 在点
在点![]() ,
,![]() 之间).
之间).
(1)求椭圆![]() 的方程;
的方程;
(2)若![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)若射线![]() 交椭圆
交椭圆![]() 于点
于点![]() (
(![]() 为原点),求
为原点),求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com