
(1)a·b=|a||b|是a∥b的充要条件;
(2)|a·b|=|a||b|是a与b共线的充要条件;
(3)|a|=|b|且|a·c|=|b·c|是a∥b的必要不充分条件;
(4)|a|=|b|且a·c=b·c是a∥b的充分不必要条件.
解析:对这四个命题进行判断时,其理论依据是向量的数量积:a·b=|a||b|cosθ(θ是a,b的夹角)及向量平行的充要条件.?
(1)∵a·b=|a||b|cosθ,a·b=|a||b|,?
? ∴cosθ=1.?
∴a与b的夹角为0°,即a与b同向.∴a∥b.?
但反过来,由a∥b可推出a与b同向或反向,?
而当a与b反向时,a与b的夹角为180°,?
这时a·b=-|a||b|,它与条件a·b=|a||b|不相等,?
故命题(1)不成立.?
(2)∵|a·b|=||a||b|cosθ|=|a||b||cosθ|,?
又∵|a·b|=|a||b|,∴|cosθ|=1.?
∴cosθ=±1.∴θ=0°或180°.?
∴a与b同向或反向. ∴a∥b.?
而以上几步均可逆,故命题(2)为真.?
(3)∵a·c=|a||c|cosα(α是a,c的夹角),b·c=|b||c|cosβ(β是b,c的夹角),?
又∵|a|=|b|且|a·c|=|b·c|, ∴|cosα|=|cosβ|.?
由它推不出α=β,故(3)为假命题.?
(4)∵a·c=b·c,?
∴|a||c|cosα=|b||c|cosβ(其中α是a,c的夹角,β是b,c的夹角).?
又∵|a|=|b|,∴cosα=cosβ.?
∴α=β(∵α,β∈[0°,180°]).?
∴a与b同向,故a∥b.?
但是反过来,由a∥b却推不出|a|=|b|,故命题为真.


科目:高中数学 来源:2013-2014学年辽宁省高三上学期期中考试理科数学试卷(解析版) 题型:选择题
已知a,b,c是三条不同的直线,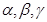 是三个不同的平面,上述命题中真命题的是
是三个不同的平面,上述命题中真命题的是
A.若a⊥c,b⊥c,则a∥b或a⊥b
B.若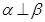 ,
,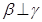 ,则
,则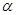 ∥
∥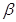 ;
;
C.若a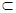
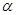 ,b
,b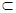
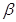 ,c
,c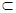
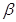 ,a⊥b, a⊥c,则
,a⊥b, a⊥c,则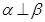 ;
;
D.若a⊥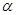 , b
, b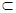
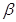 ,a∥b,则
,a∥b,则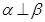
查看答案和解析>>
科目:高中数学 来源: 题型:
已知a,b,c是空间三条直线,α、β是两个平面,则下列命题中不正确的是
A.若a∥b,b∥α,则a∥α或a![]() α
α
B.若a⊥α,b⊥β,α∥β,则a∥b
C.若a∥b,α∥β,则a与α所成的角等于b与β所成的角
D.若a⊥b,a⊥c,则b∥c
查看答案和解析>>
科目:高中数学 来源: 题型:
下列命题:①若![]() ,则
,则![]() ;
;
②与非零向量![]() 共线的单位向量是
共线的单位向量是![]() ;
;
③若![]() ,则A,B,C是一个三角形的三个顶点;
,则A,B,C是一个三角形的三个顶点;
④若![]() ,则
,则![]() 至少有一个是
至少有一个是![]() ;
;
⑤已知A,B,C是不共线的三点,G是![]() 内一点,若
内一点,若![]() ,则G是
,则G是![]() 的重心。其中真命题的个数是( )
的重心。其中真命题的个数是( )
A. ![]() 个 B.
个 B.![]() 个 C.
个 C. ![]() 个 D.
个 D.![]() 个
个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com