
已知函数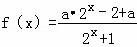 (a∈R).(1)试判断f(x)的单调性,并证明你的结论;(2)若f(x)为定义域上的奇函数,①求函数f(x)的值域;②求满足f(ax)<f(2a﹣x2)的x的取值范围.
(a∈R).(1)试判断f(x)的单调性,并证明你的结论;(2)若f(x)为定义域上的奇函数,①求函数f(x)的值域;②求满足f(ax)<f(2a﹣x2)的x的取值范围.
解:(1)函数f(x)为定义域(﹣∞,+∞),且 ,任取x1,x2∈(﹣∞,+∞),且x1<x2则
,任取x1,x2∈(﹣∞,+∞),且x1<x2则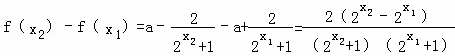 ∵y=2x在R上单调递增,且x1<x2
∵y=2x在R上单调递增,且x1<x2
∴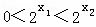 ,
,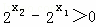 ,
, ,
,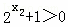 ,∴f(x2)﹣f(x1)>0,即f(x2)>f(x1),∴f(x)在(﹣∞,+∞)上的单调增函数.…(5分)(2)∵f(x)是定义域上的奇函数,∴f(﹣x)=﹣f(x),即
,∴f(x2)﹣f(x1)>0,即f(x2)>f(x1),∴f(x)在(﹣∞,+∞)上的单调增函数.…(5分)(2)∵f(x)是定义域上的奇函数,∴f(﹣x)=﹣f(x),即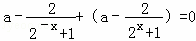 对任意实数x恒成立,化简得
对任意实数x恒成立,化简得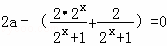 ,∴2a﹣2=0,即a=1,…(8分)(注:直接由f(0)=0得a=1而不检验扣2分)①由a=1得
,∴2a﹣2=0,即a=1,…(8分)(注:直接由f(0)=0得a=1而不检验扣2分)①由a=1得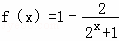 ,∵2x+1>1,∴
,∵2x+1>1,∴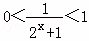 ,…(10分)∴
,…(10分)∴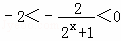 ,∴
,∴ 故函数f(x)的值域为(﹣1,1).…(12分)
故函数f(x)的值域为(﹣1,1).…(12分)
②由a=1,得f(x)<f(2﹣x2),∵f(x)在(﹣∞,+∞)上单调递增,∴x<2﹣x2,…(14分)解得﹣2<x<1,
故x的取值范围为(﹣2,1).…(16分)


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:
已知等比数列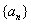 的前10项的积为32,则以下说法中正确的个数是( )
的前10项的积为32,则以下说法中正确的个数是( )
①数列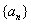 的各项均为正数; ②数列
的各项均为正数; ②数列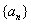 中必有小于
中必有小于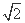 的项;
的项;
③数列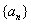 的公比必是正数; ④数列
的公比必是正数; ④数列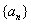 中的首项和公比中必有一个大于1.
中的首项和公比中必有一个大于1.
A.1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:高中数学 来源: 题型:
定义在R上的偶函数f(x)满足f(2﹣x)=f(x),且在[﹣3,﹣2]上是减函数,α,β是钝角三角形的两个锐角,则下列结论正确的是( )
|
| A. | f(sinα)>f(cosβ) | B. | f(cosα)<f(cosβ) | C. | f(cosα)>f(cosβ) | D. | f(sinα)<f(cosβ) |
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=x﹣[x],其中[x]表示不超过实数x的最大整数.若关于x的方程f(x)=kx+k有三个不同的实根,则实数k的取值范围是( )
|
| A. |
| B. |
| C. |
| D. |
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com