
 在边长为a的正方形ABCD中,E,F分别为BC,CD的中点,现沿AE、AF、EF折叠,使B、C、D三点重合,构成一个三棱锥B-AEF,如图所示.
在边长为a的正方形ABCD中,E,F分别为BC,CD的中点,现沿AE、AF、EF折叠,使B、C、D三点重合,构成一个三棱锥B-AEF,如图所示. .…..(8分)
.…..(8分) ,
,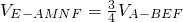 .…..(10分)
.…..(10分) ,
, ,
, .…..(13分)
.…..(13分) .因为三棱锥E-ABF与四棱锥E-AMNF的高相等,所以,四棱锥E-AMNF的体积是三棱锥E-ABF的体积的
.因为三棱锥E-ABF与四棱锥E-AMNF的高相等,所以,四棱锥E-AMNF的体积是三棱锥E-ABF的体积的 ,因为VE-ABF=VA-BEF,所以
,因为VE-ABF=VA-BEF,所以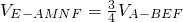 .由此能够求出四棱锥E-AMNF的体积.
.由此能够求出四棱锥E-AMNF的体积.

科目:高中数学 来源: 题型:
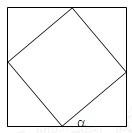 在边长为a的正方形ABCD中内依次作内接正方形AiBiCiDi(i=1,2,3,…),使内接正方形与相邻前一个正方形的一边夹角为a,求所有正方形的面积之和.
在边长为a的正方形ABCD中内依次作内接正方形AiBiCiDi(i=1,2,3,…),使内接正方形与相邻前一个正方形的一边夹角为a,求所有正方形的面积之和.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,在边长为a的正方形组成的网格中,设椭圆C1、C2、C3的离心率分别为e1、e2、e3,则e1、e2、e3的关系为
如图所示,在边长为a的正方形组成的网格中,设椭圆C1、C2、C3的离心率分别为e1、e2、e3,则e1、e2、e3的关系为查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•海淀区二模)如图,在边长为a的正方形内有不规则图形Ω.向正方形内随机撒豆子,若撒在图形Ω内和正方形内的豆子数分别为m,n,则图形Ω面积的估计值为( )
(2013•海淀区二模)如图,在边长为a的正方形内有不规则图形Ω.向正方形内随机撒豆子,若撒在图形Ω内和正方形内的豆子数分别为m,n,则图形Ω面积的估计值为( )查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在边长为a的正方形ABCD中内依次作内接正方形AiBiCiDi(i=1,2,3,…),使内接正方形与相邻前一个正方形的一边夹角为a,求所有正方形的面积之和.
在边长为a的正方形ABCD中内依次作内接正方形AiBiCiDi(i=1,2,3,…),使内接正方形与相邻前一个正方形的一边夹角为a,求所有正方形的面积之和.查看答案和解析>>
科目:高中数学 来源:高考数学一轮复习必备(第92-93课时):第十二章 极限-数列的极限、数学归纳法(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com