
已知双曲线的中心在原点,焦点F1,F2在坐标轴上,离心率为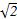
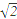 ,且过点P(4,-
,且过点P(4,-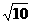 ).
).
(1)求双曲线的方程.
(2)若点M(3,m)在双曲线上,求证: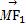
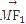 ·
·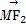
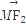 =0.
=0.
(3)求△F1MF2的面积.
1)∵e=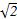
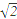 ,
,
∴可设双曲线方程为x2-y2=λ(λ≠0).
∵过点P(4,-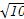
 ),∴16-10=λ,即λ=6.
),∴16-10=λ,即λ=6.
∴双曲线方程为x2-y2=6.
(2)方法一:由(1)可知,双曲线中a=b=
 ,
,
∴c=2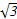
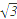 ,∴F1(-2
,∴F1(-2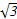
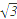 ,0),F2(2
,0),F2(2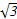
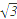 ,0).
,0).
∴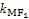
 =
=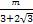
 ,
,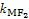
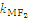 =
=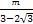
 ,
,
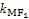
 ·
·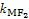
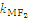 =
=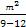
 =-
=-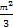
 .
.
∵点M(3,m)在双曲线上,
∴9-m2=6,m2=3.
故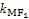
 ·
·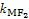
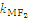 =-1,∴MF1⊥MF2.
=-1,∴MF1⊥MF2.
∴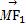
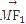 ·
·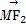
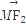 =0.
=0.
方法二:∵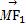
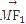 =(-3-2
=(-3-2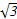
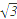 ,-m),
,-m),
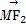
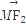 =(2
=(2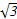
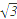 -3,-m),
-3,-m),
∴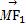
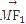 ·
·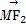
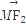 =(3+2
=(3+2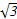
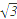 )×(3-2
)×(3-2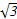
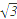 )+m2=-3+m2.
)+m2=-3+m2.
∴9-m2=6,即m2-3=0.∴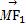
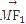 ·
·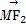
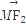 =0.
=0.
(3)△F1MF2的底|F1F2|=4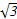
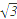 ,
,
△F1MF2的边F1F2的高h=|m|=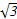
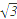 ,∴
,∴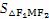
 =6.∵M(3,m)在双曲线上,
=6.∵M(3,m)在双曲线上,


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源: 题型:
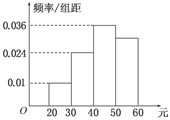
学校为了调查学生在课外读物方面的支出情况,抽出了一个容量为n且支出在[20,60)元的样本,其频率分布直方图如右图,其中支出在[50,60)元的同学有30人,则n的值为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
为得到函数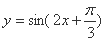 的导函数图象,只需把函数
的导函数图象,只需把函数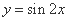 的图象上所有点的
的图象上所有点的
A.纵坐标伸长到原来的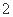 倍,横坐标向左平移
倍,横坐标向左平移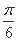
B.纵坐标缩短到原来的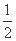 倍,横坐标向左平移
倍,横坐标向左平移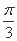
C.纵坐标伸长到原来的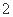 倍,横坐标向左平移
倍,横坐标向左平移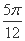
D.纵坐标缩短到原来的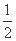 倍,横坐标向左平移
倍,横坐标向左平移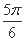
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com