
【题目】已知函数![]() ,
,![]() .
.
(1)若曲线![]() 与
与![]() 在点
在点![]() 处有相同的切线,求函数
处有相同的切线,求函数![]() 的极值;
的极值;
(2)若![]() ,讨论函数
,讨论函数![]() 的单调性.
的单调性.
【答案】(1)![]() 的极大值
的极大值![]() ,极小值为
,极小值为![]() ;(2)
;(2)![]() 时,
时,![]() 的单调增区间为
的单调增区间为![]() ,单调减区间为
,单调减区间为![]() ;
;![]() 时,
时,![]() 的单调增区间为
的单调增区间为![]() ,
,![]() ,单调减区间为
,单调减区间为![]() ;
;![]() 时,
时,![]() 的单调增区间为
的单调增区间为![]() ,没有减区间;
,没有减区间;![]() 时,
时,![]() 的单调增区间为
的单调增区间为![]() ,
,![]() ,单调减区间为
,单调减区间为![]() .
.
【解析】
(1)对函数![]() ,
,![]() 分别求导,根据曲线
分别求导,根据曲线![]() 与
与![]() 在点
在点![]() 处有相同的切线,可知
处有相同的切线,可知![]() ,解得
,解得![]() ,从而得到
,从而得到![]() ,求
,求![]() ,判断导数的正负,求极值,即可.
,判断导数的正负,求极值,即可.
(2)先求![]() 的定义域,求导数
的定义域,求导数![]() ,对
,对![]() 进行分类讨论,求解即可.
进行分类讨论,求解即可.
(1)![]() ,
,![]()
![]() ,
,![]() ,
,
由题意知![]() ,∴
,∴![]() ,
,
∴![]()
∴![]() ,
,
∴![]()
∴![]() 或
或![]() 时,
时,![]() ,
,![]() 时,
时,![]() ,
,
∴![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数,在
上是减函数,在![]() 上是增函数,
上是增函数,
∴![]() 的极大值
的极大值![]() ,极小值为
,极小值为![]() .
.
(2)![]() 的定义域为
的定义域为![]() ,
,
![]()
![]() ,
,
当![]() 时,∵
时,∵![]() ,∴
,∴![]() .
.
∴![]() 时,
时,![]() ,
,![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() 的解集为
的解集为![]() ,
,![]() 解集为
解集为![]() ,
,
当![]() 时,
时,![]() ,当
,当![]() 时取等号,
时取等号,
当![]() 时,
时,![]() 解集为
解集为![]() ,
,![]() 解集为
解集为![]() ,
,
∴![]() 时,
时,![]() 的单调增区间为
的单调增区间为![]() ,单调减区间为
,单调减区间为![]() ,
,
![]() 时,
时,![]() 的单调增区间为
的单调增区间为![]() ,
,![]() ,单调减区间为
,单调减区间为![]() ,
,
![]() 时,
时,![]() 的单调增区间为
的单调增区间为![]() ,没有减区间,
,没有减区间,
![]() 时,
时,![]() 的单调增区间为
的单调增区间为![]() ,
,![]() ,单调减区间为
,单调减区间为![]() .
.


科目:高中数学 来源: 题型:
【题目】某公司生产一种产品,每年投入固定成本0.5万元,此外每生产100件这种产品还需要增加投资0.25万元,经预测可知,市场对这种产品的年需求量为500件,当出售的这种产品的数量为t(单位:百件)时,销售所得的收入约为![]() (万元).
(万元).
(1)若该公司的年产量为x(单位:百件),试把该公司生产并销售这种产品所得的年利润表示为年产量x的函数;
(2)当这种产品的年产量为多少时,当年所得利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中正确的有( )
A.设正六棱锥的底面边长为1,侧棱长为![]() ,那么它的体积为
,那么它的体积为![]()
B.用斜二测法作△ABC的水平放置直观图得到边长为a的正三角形,则△ABC面积为![]()
C.三个平面可以将空间分成4,6,7或者8个部分
D.已知四点不共面,则其中任意三点不共线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知奇函数f(x)![]() ,函数g(θ)=cos2θ+2sinθ
,函数g(θ)=cos2θ+2sinθ![]() ,θ∈[m,
,θ∈[m,![]() ].m,b∈R.
].m,b∈R.
(1)求b的值;
(2)判断函数f(x)在[0,1]上的单调性,并证明;
(3)当x∈[0,1]时,函数g(θ)的最小值恰为f(x)的最大值,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
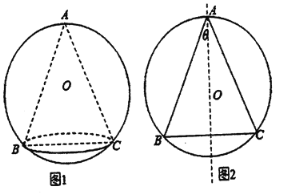
【题目】某艺术品公司欲生产一款迎新春工艺礼品,该礼品是由玻璃球面和该球的内接圆锥组成,圆锥的侧面用于艺术装饰,如图1.为了便于设计,可将该礼品看成是由圆O及其内接等腰三角形![]() 绕底边
绕底边![]() 上的高所在直线
上的高所在直线![]() 旋转
旋转![]() 而成,如图2.已知圆O的半径为
而成,如图2.已知圆O的半径为![]() ,设
,设![]() ,
,![]() ,圆锥的侧面积为
,圆锥的侧面积为![]() (S圆锥的侧面积
(S圆锥的侧面积![]() (R-底面圆半径,I-母线长))
(R-底面圆半径,I-母线长))
(1)求S关于![]() 的函数关系式;
的函数关系式;
(2)为了达到最佳观赏效果,要求圆锥的侧面积S最大.求S取得最大值时腰![]() 的长度
的长度
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代的数学名著,书中有如下问题:“今有五人分五钱,令上两人所得与下三人等。问各得几何?”其意思是:“已知甲、乙、丙、丁、戊五人分五钱,甲、乙两人所得之和与丙、丁、戊三人所得之和相等,且甲、乙、丙、丁、戊所得依次成等差数列。问五人各得多少钱?”(“钱”是古代的一种重量单位)。这个问题中,戊所得为( )
A. ![]() 钱 B.
钱 B. ![]() 钱 C.
钱 C. ![]() 钱 D.
钱 D. ![]() 钱
钱
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com