
解:(I)a=2时,令f(x)=g(x)可得 x
2+3x+1=
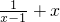
,整理可得 x
3+x
2-x-2=0 (x≠1).
令y=x
3+x
2-x-2=0 (x≠1),它的导数为y′=3x
2+2x-1,令y′=0,可得 x
1=-1,
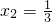
.
故函数y的极值点在-1和

处,且两个极值都是负数,故函数y与x轴的交点只有一个,故y=f(x)和y=g(x)的公共点只有一个.
(II)联立y=f(x)和y=g(x)得 x
2+3x+1=
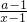
+x,整理可得 a=x
3+x
2-x,且 x≠1.
令函数h(x)=x
3+x
2-x,可得函数h(x) 的极值点在-1和

处,画出h(x)的草图,
当x=-1时,h(x)=1; 当x=

时,h(x)=
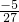
.
故当a=1时,y=a和y=h(x)仅有一个交点,因为(1,1)不在h(x)上,不满足条件.
故当a=
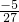
时,结合图象可得y=a和y=h(x)恰有2个交点.
综上,只有当a=
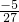
时,才能满足y=a和y=h(x)恰有2个交点.
分析:(I)a=2时,令f(x)=g(x)可得x
3+x
2-x-2=0(x≠1),令y=x
3+x
2-x-2=0 (x≠1),根据它的导数判断函数y的极值点在-1和

处,且两个极值都是负数,故y=f(x)和y=g(x)的公共点只有一个.
(II)联立y=f(x)和y=g(x)得 a=x
3+x
2-x,且 x≠1,画出函数h(x)=x
3+x
2-x 的草图,求出h(x) 的极值,可得当a=
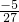
时,y=a和y=h(x)恰有2个交点.
点评:本题主要考查方程根的存在性以及个数的判断方法,体现了数形结合的数学思想,属于中档题.

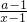 +x.
+x. 解:(I)a=2时,令f(x)=g(x)可得 x2+3x+1=
解:(I)a=2时,令f(x)=g(x)可得 x2+3x+1=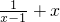 ,整理可得 x3+x2-x-2=0 (x≠1).
,整理可得 x3+x2-x-2=0 (x≠1).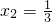 .
. 处,且两个极值都是负数,故函数y与x轴的交点只有一个,故y=f(x)和y=g(x)的公共点只有一个.
处,且两个极值都是负数,故函数y与x轴的交点只有一个,故y=f(x)和y=g(x)的公共点只有一个.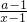 +x,整理可得 a=x3+x2-x,且 x≠1.
+x,整理可得 a=x3+x2-x,且 x≠1. 处,画出h(x)的草图,
处,画出h(x)的草图, 时,h(x)=
时,h(x)=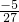 .
.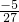 时,结合图象可得y=a和y=h(x)恰有2个交点.
时,结合图象可得y=a和y=h(x)恰有2个交点.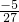 时,才能满足y=a和y=h(x)恰有2个交点.
时,才能满足y=a和y=h(x)恰有2个交点. 处,且两个极值都是负数,故y=f(x)和y=g(x)的公共点只有一个.
处,且两个极值都是负数,故y=f(x)和y=g(x)的公共点只有一个.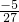 时,y=a和y=h(x)恰有2个交点.
时,y=a和y=h(x)恰有2个交点.
