

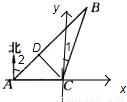
 解:作CD⊥AB,垂足为D.
解:作CD⊥AB,垂足为D.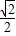 =15
=15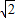 (海里).
(海里).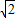 ,
, (海里).
(海里).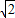 海里.
海里.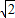 .
.

科目:高中数学 来源: 题型:
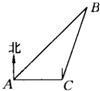 如图所示,一艘轮船在A处观测到北偏东45°方向上有一个灯塔B,轮船在正东方向以每小时20海里的速度航行1.5小时后到达C处,又观测到灯塔B在北偏东15°方向上,则此时轮船与灯塔B相距
如图所示,一艘轮船在A处观测到北偏东45°方向上有一个灯塔B,轮船在正东方向以每小时20海里的速度航行1.5小时后到达C处,又观测到灯塔B在北偏东15°方向上,则此时轮船与灯塔B相距
查看答案和解析>>
科目:高中数学 来源: 题型:
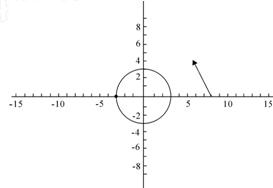 一艘轮船在沿直线返回港口的途中,接到气象台的台风预报:台风中心位于轮船正西80km处,受影响的范围是半径长为r(r>0)km的圆形区域.轮船的航行方向为西偏北45°且不改变航线,假设台风中心不移动. 如图所示,试问:
一艘轮船在沿直线返回港口的途中,接到气象台的台风预报:台风中心位于轮船正西80km处,受影响的范围是半径长为r(r>0)km的圆形区域.轮船的航行方向为西偏北45°且不改变航线,假设台风中心不移动. 如图所示,试问:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
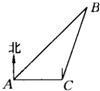 如图所示,一艘轮船在A处观测到北偏东45°方向上有一个灯塔B,轮船在正东方向以每小时20海里的速度航行1.5小时后到达C处,又观测到灯塔B在北偏东15°方向上,则此时轮船与灯塔B相距 ________海里.(结果保留根号)
如图所示,一艘轮船在A处观测到北偏东45°方向上有一个灯塔B,轮船在正东方向以每小时20海里的速度航行1.5小时后到达C处,又观测到灯塔B在北偏东15°方向上,则此时轮船与灯塔B相距 ________海里.(结果保留根号)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
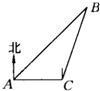
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com