
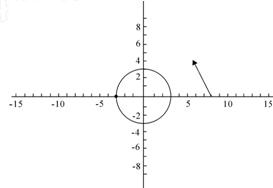
 一艘轮船在沿直线返回港口的途中,接到气象台的台风预报:台风中心位于轮船正西80km处,受影响的范围是半径长为r(r>0)km的圆形区域.轮船的航行方向为西偏北45°且不改变航线,假设台风中心不移动. 如图所示,试问:
一艘轮船在沿直线返回港口的途中,接到气象台的台风预报:台风中心位于轮船正西80km处,受影响的范围是半径长为r(r>0)km的圆形区域.轮船的航行方向为西偏北45°且不改变航线,假设台风中心不移动. 如图所示,试问:| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
602-(40
|


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2012年苏教版高中数学必修2 2.2圆的方程练习卷(解析版) 题型:解答题
(12分)一艘轮船在沿直线返回港口的途中,接到气象台的台风预报:台风中心位于轮船正西70 km处,受影响的范围是半径长30 km的圆形区域.已知港口位于台风正北40 km处,如果这艘轮船不改变航线,那么它是否会受到台风的影响?
查看答案和解析>>
科目:高中数学 来源:浙江省期末题 题型:解答题
 km的圆形区域。轮船的航行方向为西偏北45°且不改变航线,假设台风中心不移动。如图所示,试问:
km的圆形区域。轮船的航行方向为西偏北45°且不改变航线,假设台风中心不移动。如图所示,试问: 
查看答案和解析>>
科目:高中数学 来源:2008-2009学年浙江省宁波市高一(下)期末数学试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com