
【题目】函数f(x)=Asin(ωx+φ),x∈R,(ω>0,﹣ ![]() <φ<
<φ< ![]() )的部分图象如图所示.
)的部分图象如图所示.
(Ⅰ)确定A,ω,φ的值,并写出函数f(x)的解析式;
(Ⅱ)描述函数y=f(x)的图象可由函数y=sinx的图象经过怎样的变换而得到;
(Ⅲ)若f( ![]() )=
)= ![]() (
( ![]() <α<
<α< ![]() ),求tan2(α﹣
),求tan2(α﹣ ![]() ).
).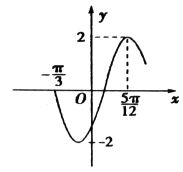
【答案】解:(Ⅰ)根据函数f(x)=Asin(ωx+φ)的图象知A=2.
∵ ![]() =
= ![]() ﹣(
﹣( ![]() ),∴T=π.∴ω=2.
),∴T=π.∴ω=2.
由五点法作图知当x= ![]() 时,ωx+φ=
时,ωx+φ= ![]() ,
,
即2× ![]() π+φ=
π+φ= ![]() ,∴φ=﹣
,∴φ=﹣ ![]() .故
.故 ![]() .
.
(Ⅱ)先把y=sinx的图象向右平移 ![]() 个单位长度得到
个单位长度得到 ![]() 的图象,
的图象,
使曲线上各点的横坐标变为原来的 ![]() ,得到函数
,得到函数 ![]() 的图象,
的图象,
最后把曲线上各点的纵坐标变为原来的2倍,得到 ![]() .
.
(Ⅲ)由 ![]() 得
得 ![]() ,因为
,因为 ![]()
所以 ![]() ,得
,得 ![]() ,故
,故 ![]() ,
,
∴ 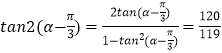 .
.
【解析】(1)根据函数图象可知A=2,由图象可读出最小正周期T=π,根据周期公式得到ω=2,又因为点(![]() ,2)在函数图象上,代入即可解出φ的值,从而得到f(x)的解析式,(2)通过函数图象的平移规则可得出平移过程,(3)根据f (
,2)在函数图象上,代入即可解出φ的值,从而得到f(x)的解析式,(2)通过函数图象的平移规则可得出平移过程,(3)根据f ( ![]() ) =
) = ![]() 得 s i n ( α
得 s i n ( α ![]() ) =
) = ![]() ,判断出α
,判断出α ![]() 的范围后,根据同角的三角函数关系得出cos(α
的范围后,根据同角的三角函数关系得出cos(α ![]() )的值,进而得到tan(α
)的值,进而得到tan(α ![]() ),结合二倍角的正切公式可得结果.
),结合二倍角的正切公式可得结果.


 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】现有4个人去参加娱乐活动,该活动有甲、乙两个游戏可供参加者选择.为增加趣味性,约定:每个人通过掷一枚质地均匀的骰子决定自己去参加哪个游戏,掷出点数为1或2的人去参加甲游戏,掷出点数大于2的人去参加乙游戏.
(1)求这4个人中恰有2人去参加甲游戏的概率;
(2)求这4个人中去参加甲游戏的人数大于去参加乙游戏的人数的概率;
(3)用X,Y分别表示这4个人中去参加甲、乙游戏的人数,记ξ=|X﹣Y|,求随机变量ξ的分布列与数学期望Eξ.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2﹣x+2a﹣1(a>0).
(1)若f(x)在区间[1,2]为单调增函数,求a的取值范围;
(2)设函数f(x)在区间[1,2]上的最小值为g(a),求g(a)的表达式;
(3)设函数 ![]() ,若对任意x1 , x2∈[1,2],不等式f(x1)≥h(x2)恒成立,求实数a的取值范围.
,若对任意x1 , x2∈[1,2],不等式f(x1)≥h(x2)恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等比数列{an}的各项都是正数,2a5 , a4 , 4a6成等差数列,且满足 ![]() ,数列{bn}的前n项和为
,数列{bn}的前n项和为 ![]() ,n∈N* , 且b1=1
,n∈N* , 且b1=1
(1)求数列{an},{bn}的通项公式
(2)设 ![]() ,n∈N* , {Cn}前n项和为
,n∈N* , {Cn}前n项和为 ![]() ,求证:
,求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() .
.
(1)计算f(3),f(4),f( ![]() )及f(
)及f( ![]() )的值;
)的值;
(2)由(1)的结果猜想一个普遍的结论,并加以证明;
(3)求值f(1)+f(2)+…+f(2017)+f( ![]() )+f(
)+f( ![]() )+…+f(
)+…+f( ![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别为角A,B,C所对的边.已知sinC= ![]() sinB,c=2,cosA=
sinB,c=2,cosA= ![]() .
.
(Ⅰ)求a的值;
(Ⅱ)求sin(2A﹣ ![]() )的值.
)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以直角坐标系的原点O为极点,x轴的正半轴为极轴建立极坐标系.
(1)将直线l: 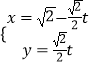 (t为参数)化为极坐标方程;
(t为参数)化为极坐标方程;
(2)设P是(1)中直线l上的动点,定点A( ![]() ,
, ![]() ),B是曲线ρ=﹣2sinθ上的动点,求|PA|+|PB|的最小值.
),B是曲线ρ=﹣2sinθ上的动点,求|PA|+|PB|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某网店经营的一种商品进价是每件10元,根据一周的销售数据得出周销量P(件)与单价x(元)之间的关系如图折线所示,该网店与这种商品有关的周开支均为25元.
(I)根据周销量图写出周销量P(件)与单价x(元)之间的函数关系式;
(Ⅱ)写出周利润y(元)与单价x(元)之间的函数关系式;当该商品的销售价格为多少元时,周利润最大?并求出最大周利润.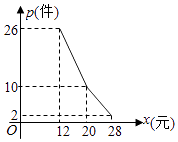
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com