球O的表面积96π,球面上有两点P、Q,过P、Q作球的截面O1,若O1P⊥O1Q,且球心O到截面PQO1的距离为4,那么球心O到PQ的距离为 .
【答案】
分析:由球的表面积为96π,我们可以根据球的表面积公式,构造关于球半径R的方程,解方程即可得到球的半径R,进而根据球心O到截面PQO
1的距离为4,我们可以求出PQ两点之间的空间距离,从而得到O
1A的长度,解三角形OAO
1后,我们可以求出球心O到PQ的距离.
解答: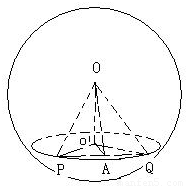
解:∵球的表面积为S=4πR
2=96π
∴R
2=24
∴R=2
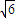
,
∵球心O到截面PQO
1的距离为4,∴OO
1=4,如图,
在直角三角形PAO
1中,PO
1=
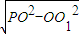
=
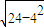
=2
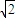
,
∵O
1P⊥O
1Q,故PQ=2
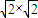
=4,O
1A=2,
∴在直角三角形OAO
1中,球心O到PQ的距离为OA=
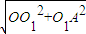
=
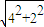
=2
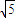
故答案为:2
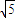
.
点评:本题考查的知识点是球的表面积公式,解三角形,其中利用弦心距,半弦长,球半径满足勾股定理求出弦长PQ的值是解答的关键.

 解:∵球的表面积为S=4πR2=96π
解:∵球的表面积为S=4πR2=96π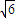 ,
,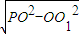 =
=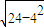 =2
=2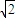 ,
,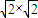 =4,O1A=2,
=4,O1A=2,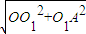 =
=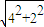 =2
=2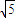
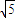 .
.

 名校课堂系列答案
名校课堂系列答案