
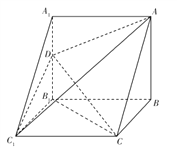
【题目】如图所示,直三棱柱![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 为棱
为棱![]() 的中点.
的中点.
(Ⅰ)探究直线![]() 与平面
与平面![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(Ⅱ)若![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】将参加数学竞赛的1000名学生编号如下:0001,0002,0003,…,1000,按系统抽样的方法从中抽取一个容量为50的样本,如果在第一组抽得的编号是0015,则在第21组抽得的编号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥P﹣ABCD,底面ABCD是直角梯形,AD∥BC,∠BCD=90°,PA⊥底面ABCD,△ABM是边长为2的等边三角形, ![]() .
. 
(1)求证:平面PAM⊥平面PDM;
(2)若点E为PC中点,求二面角P﹣MD﹣E的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的一个焦点与上、下顶点构成直角三角形,以椭圆
的一个焦点与上、下顶点构成直角三角形,以椭圆![]() 的长轴长为直径的圆与直线
的长轴长为直径的圆与直线![]() 相切.
相切.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设过椭圆右焦点且不平行于![]() 轴的动直线与椭圆
轴的动直线与椭圆![]() 相交于
相交于![]() 两点,探究在
两点,探究在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() 为定值?若存在,试求出定值和点
为定值?若存在,试求出定值和点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某矩形花坛ABCD长AB=3m,宽AD=2m,现将此花坛在原有基础上有拓展成三角形区域,AB、AD分别延长至E、F并使E、C、F三点共线. 
(1)要使三角形AEF的面积大于16平方米,则AF的长应在什么范围内?
(2)当AF的长度是多少时,三角形AEF的面积最小?并求出最小面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某教师调查了![]() 名高三学生购买的数学课外辅导书的数量,将统计数据制成如下表格:
名高三学生购买的数学课外辅导书的数量,将统计数据制成如下表格:
男生 | 女生 | 总计 | |
购买数学课外辅导书超过 |
|
|
|
购买数学课外辅导书不超过 |
|
|
|
总计 |
|
|
|
(Ⅰ)根据表格中的数据,是否有![]() 的把握认为购买数学课外辅导书的数量与性别相关;
的把握认为购买数学课外辅导书的数量与性别相关;
(Ⅱ)从购买数学课外辅导书不超过![]() 本的学生中,按照性别分层抽样抽取
本的学生中,按照性别分层抽样抽取![]() 人,再从这
人,再从这![]() 人中随机抽取
人中随机抽取![]() 人询问购买原因,求恰有
人询问购买原因,求恰有![]() 名男生被抽到的概率.
名男生被抽到的概率.
附:  ,
, ![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在等腰直角三角形ABC中,AB=AC=4,点P是边AB边上异于AB的一点,光线从点P出发,经BC,CA反射后又回到点P(如图),若光线QR经过△ABC的重心,则AP等于( )
A.2
B.1
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com