
【题目】设Sn为数列{an}的前n项和,Sn=2n2﹣30n.
(1)求a1及an;
(2)判断这个数列是否是等差数列.
【答案】
(1)解:由Sn=2n2﹣30n,得 ![]() ,
,
当n≥2时,an=Sn﹣Sn﹣1=2n2﹣30n﹣[2(n﹣1)2﹣30(n﹣1)]=4n﹣32.
验证n=1上式成立,
∴an=4n﹣32
(2)解:由an=4n﹣32,得an﹣1=4(n﹣1)﹣32(n≥2),
∴an﹣an﹣1=4n﹣32﹣[4(n﹣1)﹣32]=4(常数),
∴数列{an}是等差数列
【解析】(1)在数列的前n项和中,取n=1求得a1 , 再由an=Sn﹣Sn﹣1(n≥2)求得an;(2)由(1)中求得的通项公式,利用定义判断数列是等差数列.
【考点精析】本题主要考查了等差关系的确定的相关知识点,需要掌握如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,即![]() -
-![]() =d ,(n≥2,n∈N
=d ,(n≥2,n∈N![]() )那么这个数列就叫做等差数列才能正确解答此题.
)那么这个数列就叫做等差数列才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市为了节约生活用水,计划在本市试行居民生活用水定额管理(即确定一个居民月均用水量标准用水量不超过a的部分按照平价收费,超过a的部分按照议价收费).为了较为合理地确定出这个标准,通过抽样获得了 100位居民某年的月均用水量(单位:t),制作了频率分布直方图. 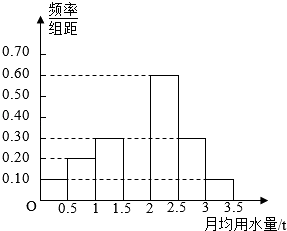
(1)由于某种原因频率分布直方图部分数据丢失,请在图中将其补充完整;
(2)用样本估计总体,如果希望80%的居民每月的用水量不超出标准则月均用水量的最低标准定为多少吨,请说明理由;
(3)从频率分布直方图中估计该100位居民月均用水量的众数,中位数,平均数(同一组中的数据用该区间的中点值代表).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】省环保研究所对某市市中心每天环境放射性污染情况进行调查研究后,发现一天中环境综合放射性污染指数![]() 与时刻
与时刻![]() (时)的关系为
(时)的关系为 ,其中
,其中![]() 是与气象有关的参数,且
是与气象有关的参数,且![]() ,若用每天
,若用每天![]() 的最大值为当天的综合放射性污染指数,并记作
的最大值为当天的综合放射性污染指数,并记作![]() .
.
(1)令![]() .求
.求![]() 的取值范围;
的取值范围;
(2)求![]() ;
;
(3)省政府规定,每天的综合放射性污染指数不得超过2,试问目前该市市中心的综合放射性污染指数是否超标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】市环保局举办2013年“六五”世界环境日宣传活动,进行现场抽奖.抽奖规则是:盒中装有10张大小相同的精美卡片,卡片上分别印有“环保会徽”或“绿色环保标志”图案.参加者每次从盒中抽取卡片两张,若抽到两张都是“绿色环保标志”卡即可获奖.
(1)活动开始后,一位参加者问:盒中有几张“绿色环保标志”卡?主持人笑说:我只知道若从盒中抽两张都不是“绿色环保标志”卡的概率是 ![]() .求抽奖者获奖的概率;
.求抽奖者获奖的概率;
(2)现有甲乙丙丁四人依次抽奖,抽后放回,另一人再抽.用ξ表示获奖的人数.求ξ的分布列及E(ξ),D(ξ).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】解答题
(1)(1)已知命题p:|x2﹣x|≥6,q:x∈Z且“p且q”与“非q”同时为假命题,求x的值.
(2)已知p:x2﹣8x﹣20≤0,q:x2﹣2x+1﹣m2≤0(m>0),若¬p是¬q的必要而不充分条件,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com