
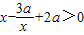 .
.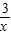 +2>0 即
+2>0 即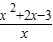 =
=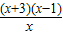 >0利用分式不等式的根轴法求解即得;
>0利用分式不等式的根轴法求解即得;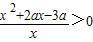 ,求出x2+2ax-3a的判别式,通过讨论判别式的情况,求出不等式的解解集.
,求出x2+2ax-3a的判别式,通过讨论判别式的情况,求出不等式的解解集.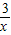 +2>0 即
+2>0 即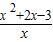 =
=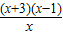 >0
>0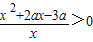 ∵x2+2ax-3a的△=4a(a+3)
∵x2+2ax-3a的△=4a(a+3)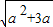 ,0)∪(
,0)∪(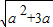 -a,+∞)
-a,+∞)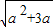 ,
,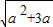 -a)
-a)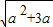 ,0)∪(
,0)∪(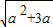 -a,+∞),
-a,+∞),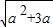 ,
,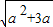 -a)(7分).
-a)(7分).

 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com