练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    正三角形ABC，点M，N，P分别为AB，BC，AC中点，沿MN，MP，NP折起，使A，B，C三点重合后为Q，则折起后二面角Q-MN-P的余弦值为（ ）

    A．
    B．
    C．
    D．
    【答案】分析：利用折起后的三棱锥是正四面体的性质、余弦定理及二面角的定义即可得出．
    解答：解：如图所示：折起的三棱锥Q-MNP为正四面体．取MN的中点O，连接QO、OP，则OQ⊥MN，OP⊥MN，
    ∴∠POQ为二面角Q-MN-P的平面角．
    不妨设MN=2，则PQ=2，OP=OQ=．
    在△OPQ中，由余弦定理可得：cos∠POQ==．
    ∴折起后二面角Q-MN-P的余弦值为．
    故选A．
    点评：熟练掌握正四面体的性质、余弦定理及二面角的定义是解题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

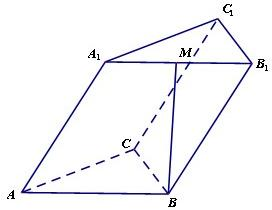    精英家教网已知斜三棱柱ABC-A1B1C1的底面是正三角形，侧面ABB1A1是边长为2的菱形，且∠A1AB=60°，M是A1B1的中点，MB⊥AC．
    ①求证：BM⊥平面ABC；
    ②求点M到平面BB1C1C的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    某同学使用类比推理得到如下结论：
    （1）同一平面内，三条不同的直线a，b，c，若a⊥c，b⊥c，则a∥b，类比出：空间中，三条不同的直线a，b，c，若a⊥c，b⊥c，则a∥b；
    （2）a，b∈R，a-b＞0则a＞b，类比出：a，b∈C，a-b＞0则a＞b；
    （3）以点（0，0）为圆心，r为半径的圆的方程是x2+y2=r2，类比出：以点（0，0，0）为球心，r为半径的球的方程是x2+y2+z2=r2；
    （4）正三角形ABC中，M是BC的中点，O是△ABC外接圆的圆心，则
    AO
    OM
    =2    ，类比出：在正四面体ABCD中，若M是△BCD的三边中线的交点，O为四面体ABCD外接球的球心，则
    AO
    OM
    =3    ．
    其中类比的结论正确的个数是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    正三角形ABC，点M，N，P分别为AB，BC，AC中点，沿MN，MP，NP折起，使A，B，C三点重合后为Q，则折起后二面角Q-MN-P的余弦值为（　　）

    查看答案和解析>>

    科目：高中数学 来源：安徽省合肥市2012届高三第二次教学质量检测数学文科试题 题型：044

    已知△ABC是边长为1的正三角形．动点M满足＝λ＋μ，且λ2＋μ2＝1．

    (1)求||最大值，并指出此时||与，的夹角；

    (2)是否存在两定点F1、F2，使．||＋||恒为常数k？若存在，指出常数k的值；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案