
【题目】如图所示,在三棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
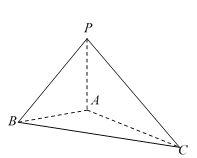
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)![]() 为棱
为棱![]() 上一点,试确定点
上一点,试确定点![]() 的位置,使得直线
的位置,使得直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
【答案】(Ⅰ)见解析;(Ⅱ) ![]() 为棱
为棱![]() 的中点
的中点
【解析】
(Ⅰ)由余弦定理得AC=![]() ,由勾股定理得PA⊥AC,由PA⊥BC,得PA⊥平面ABC,由此能证明平面ABC⊥平面PAC.
,由勾股定理得PA⊥AC,由PA⊥BC,得PA⊥平面ABC,由此能证明平面ABC⊥平面PAC.
(Ⅱ)设BC的中点为D,连结AD,以AB,AD,AP所在直线分别为x轴,y轴,z轴,建立空间直角坐标系,利用向量能求出E为棱AC的中点.
(Ⅰ)在![]() 中,由余弦定理得
中,由余弦定理得![]()
![]() ,即
,即![]() ,
,
又![]() ,
,![]() ,
,![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() 平面
平面![]() .
.
(Ⅱ)设![]() 的中点为
的中点为![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,又
,又![]() ,
,![]() .
.
如图所示,以![]() 所在直线分别为
所在直线分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() .
.
则![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设![]() (
(![]() ),则
),则![]()
设平面![]() 的法向量为
的法向量为![]() ,则
,则 ,令
,令![]() ,可得
,可得![]() ,
,
![]() ,设直线
,设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
则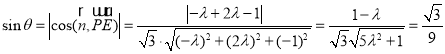 ,
,
整理得![]() ,
,![]() ,
,![]() ,
,![]() 为棱
为棱![]() 的中点.
的中点.



 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:
【题目】某校进入高中数学竞赛复赛的学生中,高一年级有8人,高二年级有16人,高三年级有32人,现釆用分层抽样的方法从这些学生中抽取7人进行釆访.
(1)求应从各年级分别抽取的人数;
(2)若从抽取的7人中再随机抽取2人做进一步了解(注高一学生记为![]() ,高二学生记为
,高二学生记为![]() ,高三学生记为
,高三学生记为![]() ,
,![]()
①列出所有可能的抽取结果;
②求抽取的2人均为高三年级学生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个口袋内装有大小相同的5个球,其中3个白球,2个黑球,从中一次摸出两个球.
(1)共有多少个基本事件?
(2)摸出的两个都是白球的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)已知双曲线的中心在原点,焦点在x轴上,实轴长为4,渐近线方程为![]() .求双曲线的标准方程;
.求双曲线的标准方程;
(2)过(1)中双曲线上一点P的直线分别交两条渐近于![]() 两点,且P是线段AB的中点,求证:
两点,且P是线段AB的中点,求证:![]() 为常数;
为常数;
(3)我们知道函数![]() 的图象是由双曲线
的图象是由双曲线![]() 的图象逆时针旋转45°得到的,函数
的图象逆时针旋转45°得到的,函数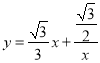 的图象也是双曲线,请尝试写出曲线
的图象也是双曲线,请尝试写出曲线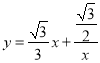 的性质(不必证明).
的性质(不必证明).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C的参数方程是![]() (
(![]() 为参数),把曲线C的横坐标缩短为原来的
为参数),把曲线C的横坐标缩短为原来的![]() ,纵坐标缩短为原来的一半,得到曲线
,纵坐标缩短为原来的一半,得到曲线![]() 直线l的普通方程是
直线l的普通方程是![]() ,以坐标原点O为极点,x轴正半轴为极轴建立极坐标系.
,以坐标原点O为极点,x轴正半轴为极轴建立极坐标系.
(1)求直线l的极坐标方程和曲线![]() 的普通方程;
的普通方程;
(2)记射线![]() (
(![]() )与
)与![]() 交于点A,与l交于点B,求
交于点A,与l交于点B,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com