练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知是双曲线的左右焦点，以为直径的圆与双曲线的一条渐近线交于点，与双曲线交于点，且均在第一象限，当直线时，双曲线的离心率为，若函数，则（）

    A. 1 B. C. 2 D.

    【答案】C

    【解析】双曲线的，双曲线的渐近线方程为与圆联立，解得，与双曲线方程联立，解得，即为，直线与直线平行时，既有，即，既有， ，即 ，故选C.

    【方法点晴】本题主要考查利用双曲线的简单性质求双曲线的离心率、双曲线的渐近线，属于难题. 求解与双曲线性质有关的问题时要结合图形进行分析，既使不画出图形，思考时也要联想到图形，当涉及顶点、焦点、实轴、虚轴、渐近线等双曲线的基本量时，要理清它们之间的关系，挖掘出它们之间的内在联系.求与离心率有关的问题，应先将 用有关的一些量表示出来，再利用其中的一些关系构造出关于e的等式.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】选修4一5:不等式选讲.

    已知函数.

    （1）求的解集；

    （2）设函数，若对任意的都成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

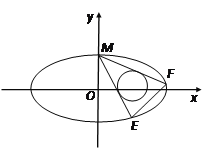
    【题目】（本题满分12分）已知椭圆C： 的离心率为， 是椭圆的两个焦点， 是椭圆上任意一点，且的周长是．

    （1）求椭圆C的方程；

    （2）设圆T： ，过椭圆的上顶点作圆T的两条切线交椭圆于E、F两点，当圆心在轴上移动且时，求EF的斜率的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，其中是自然对数的底数.

    （1）证明：当时， ；

    （2）设为整数，函数有两个零点，求的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在正四棱锥中，已知异面直线与所成的角为，给出下面三个命题:

    :若，则此四棱锥的侧面积为；

    ：若分别为的中点，则平面；

    :若都在球的表面上，则球的表面积是四边形面积的倍.

    在下列命题中，为真命题的是（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆锥曲线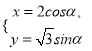： （为参数）和定点， ， 是此圆锥曲线的左、右焦点．

    （1）以原点为极点，以轴的正半轴为极轴建立极坐标系，求直线的极坐标方程；

    （2）经过且与直线垂直的直线交此圆锥曲线于， 两点，求的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f(x)是定义在[－1,1]上的奇函数，在[0,1]上f(x)＝2x＋ln(x＋1)－1.

    (1)求函数f(x)的解析式；并判断f(x)在[－1,1]上的单调性(不要求证明)；

    (2)解不等式f(2x－1)＋f(1－x2)≥0.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

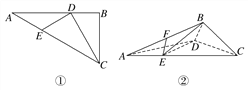
    【题目】如图①所示，在Rt△ABC中，AC＝6，BC＝3，∠ABC＝90°，CD为∠ACB的平分线，点E在线段AC上，CE＝4，将△BCD沿CD折起，使得平面BCD⊥平面ACD，连接AB，BE，如图②所示，设点F是AB的中点．

    (1)求证：DE⊥平面BCD；

    (2)若EF∥平面BDG，其中G为AC上一点，求三棱锥B－DEG的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某单位200名职工的年龄分布情况如图，现要从中抽取40名职工作样本．用系统抽样法，将全体职工随机按1～200编号，并按编号顺序平均分为40组(1～5号，6～10号，…，196～200号)．若第5组抽出的号码为22，则第8组抽出的号码应是________．若用分层抽样法，则40岁的以下的年龄段应抽取__________人．

    查看答案和解析>>

    同步练习册答案