将正偶数集合{2,4,6,…}从小到大按第n组有2n-1个偶数进行分组,{2},{4,6,8},{10,12,14,16,18},…第一组、第二组、第三组,则2010位于第组.( )
A.30
B.31
C.32
D.33
【答案】
分析:每个集合都除2,原题简化为:将正偶数集合{2,4,6,…}从小到大按第n组有2n-1个偶数进行分组,{1},{2,3,4},{5,6,7,8,9},…第一组、第二组、第三组,则1005位于第几组.设每一组的元素个数用数列{a
n}表示,根据等差数列的性质可知Sn=
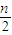
[1+1+(n-1)×2]=n
2.由31
2=961<1005<32
2=1024,可知答案.
解答:解:把,{2},{4,6,8},{10,12,14,16,18},…每个集合都除2,原题简化为:将正偶数集合{2,4,6,…}从小到大按第n组有2n-1个偶数进行分组,{1},{2,3,4},{5,6,7,8,9},…第一组、第二组、第三组,则1005位于第几组.
运用等差数列:a
n=a
1+(n-1)d,
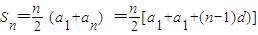
,
把每一组的元素个数用数列{a
n}表示,则a
1=1,a
2=3,a
3=5,…,公差d=2.
∴Sn=
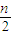
[1+1+(n-1)×2]=n
2.
∵31
2=961<1005<32
2=1024,1005-961=44
∴2010位于第32组的第44位.
故选C.
点评:本题考查数列的性质及其综合运用,解题时要注意公式的灵活运用.

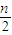 [1+1+(n-1)×2]=n2.由312=961<1005<322=1024,可知答案.
[1+1+(n-1)×2]=n2.由312=961<1005<322=1024,可知答案.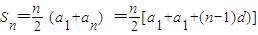 ,
,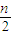 [1+1+(n-1)×2]=n2.
[1+1+(n-1)×2]=n2.
